  |
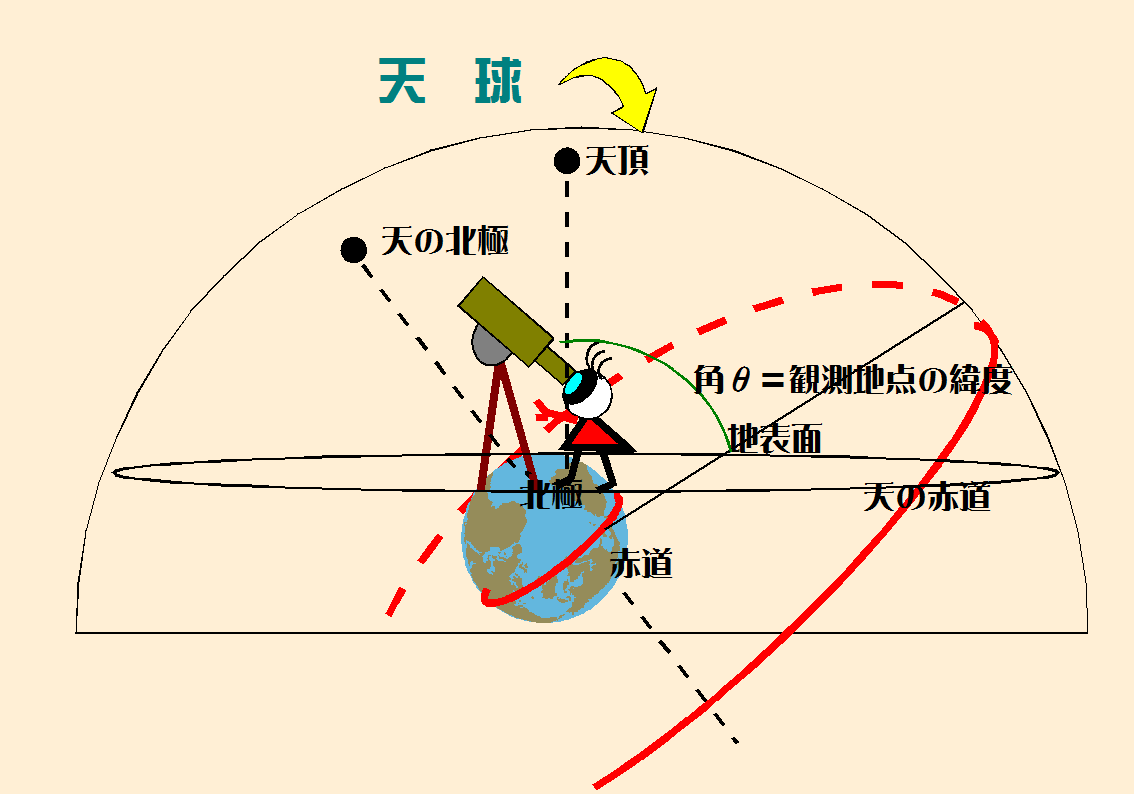
図-1
|
ひとみちゃんが何か星か銀河か望遠鏡で観察をしている。地形図であれば、等高線を用いて山の高さを表現するが、天球で
は天体の「奥行き」=「高さ」=「地球からの距離」を無視してしまう。
そのため、地球を取り巻いて半径無限大で作った「天球」を考え、そこに天体を張り付いているものとする。天体それぞれの距離
を無視し、天体相互の位置関係をことさらに取り上げようとするのである。
地球の北極(南極)を延長していき、天球との交点を「天の北極(天の南極)」、観測者(図-1 ひとみちゃん)の足と頭を延長した
直線が、天球と交わった点が「天頂」、天頂の180°反対(真下、真逆の地点)が「天底」となる。地球の赤道(面)を延長し、天球との
交線(円)を「天の赤道」。
天球は半径無限大で作っているので、地球の大きさは無視できる大きさになり、観測者は地球の中心=天球の中心にいて観測する
ことになる(図-2)。
|
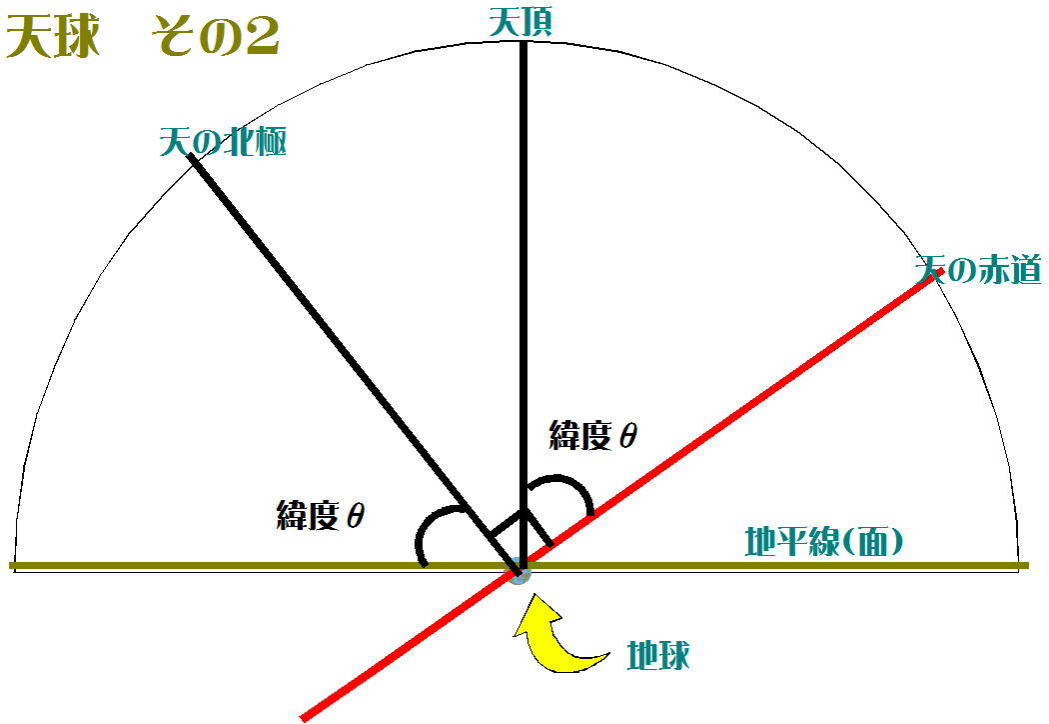
図-2
|
図-2において、∠天の赤道-観測地点(地心)-天頂は、観測地点の緯度(北緯)に等しくなる。(図-1と良く見比べて下さい)また、
∠天の北極-観測地点(地心)-地平面、つまり「天の北極の地平からの高度は、観測地点の緯度(北緯)に等しい。よく、「北極星の
高度を測れば、緯度を知ることができる」-というのはこのことなんです。
子午線とは
むかし中国では方位を十二支で現し、真北を「子(ね)」、真南を「午(うま)」と呼んだ 。天球の「天の北極」、「天頂」、
「天の南極」を通る大円を子午線といい、天体が子午線に一致したとき「南中」、特に太陽が子午線に一致したときは「正午」という。
天球 練習問題
フランスのパリは北緯49°である。
(1)天の北極の高度は何度か?
(2)また、春分(秋分)には太陽は天の赤道上に位置する。春分(秋分)の日、パリの正午の太陽高度は何度か?
天球の図を描いて答えよ。
【解答・解説】
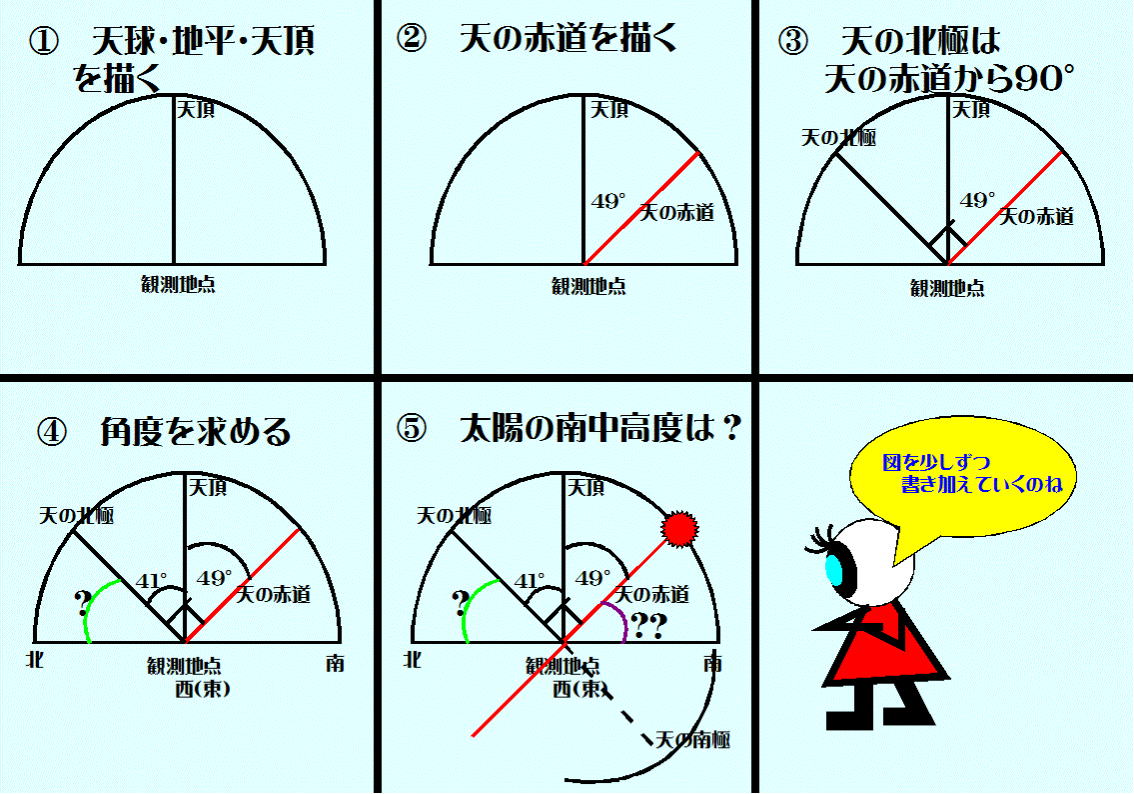
図-3
天球や赤道座標の問題は必ず問題文に示されるデータをある程度正確に図示すること。そうすることによって問題の「見える化」がなされる。
① まず、地表から半分上だけ作図する。(地面より下は見えないから)天頂方向と地平線(面)は90°で交わっている。(図-3 ①)
② 天の赤道を描く。∠天の赤道-観測地点(観測者)-天頂=観測地点(観測者)の緯度 であった。(図-1、図-2の説明)
したがって、天頂から49°に天の赤道を描く。(作図の際に、向かって左に描いてもかまわない。南北が左右反対になるだけである)
③ 天の北極は天の赤道と90°で交わるから、その角度で作図する。
④ 図から分かるように、
∠天の北極-観測地点-天頂=90°-49°=41°となる。
問われている「(1)天の北極の高度は何度か?」は図-3 ④の ∠? 。
ここまでくればお分かりでしょうが、
∠?=90°-41°=49°((1)の答え)-つまり観測地点のパリの緯度に等しい。
⑤ 春分(秋分)の正午には太陽は、「天の赤道上」かつ「子午線上」に位置するので、図-3 ⑤のようになる。
「(2)パリの正午の太陽高度」は、図-3 ⑤では∠??で示される。
∠??=90°-49°=41°((2)の答え)
 1太陽日と1恒星日 1太陽日と1恒星日 
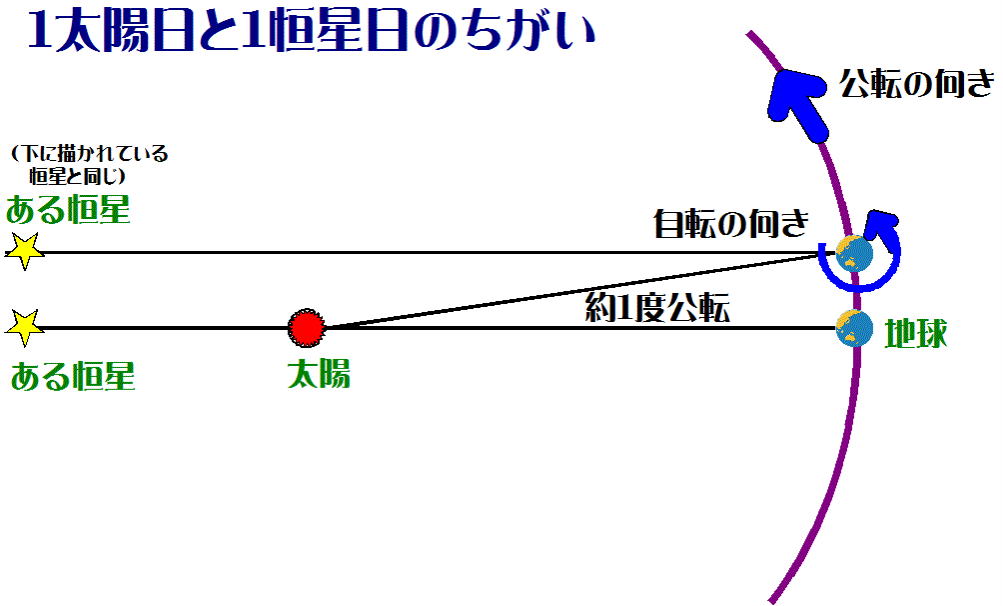
図-4
1太陽日
「一日」と言えば、日(太陽)が出て、次の日また日が出るまで-漠然とそう思っている(1太陽日)。
1恒星日
では星が出て、次の日星が出るまで同じ「一日」(1恒星日)かと思っていると、そうではない。
太陽を基準にした一日と、恒星を基準にした一日に違いがあるのは、地球が太陽の周りを公転しているために起こってくる。
図-4のようにある日、ある恒星-太陽が、地球上のある地点(P(図-4には表示されていません))で南中した-とする。
地球は太陽から半径約1.5億kmの円(詳しくは楕円)軌道を描いて公転している。地球に最も近い恒星でも4.3光年で太陽にくら
べれば、気が遠くなるほど遠くにある。したがって、恒星からやってくる光=恒星の見える方向は、地球がどこへ公転し
て移動しようが、図-4のスタートした方向に、常に平行にあるとして差し支えない。
地球は365日で360°1公転するので、1日角度にして約1度公転することになる。
約1日後、「ある恒星は、太陽より先に南中する」(図-5 参照)
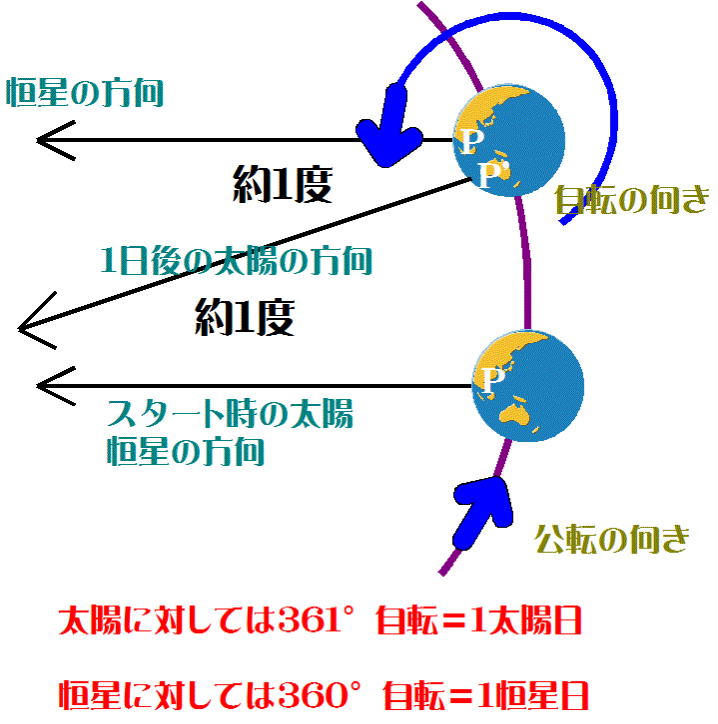
図-5
図-5 P点は恒星に対しては360°自転、「ある恒星」は再び南中したが、太陽が南中するにはP 'まで約1°余計に自転しな
ければならない。
つまり太陽に対して、361°自転をもって、24時間=1太陽日としている。
したがって、1恒星日=360°自転÷ 361°自転✕ 24時間=23.9335時間=23時間56分(詳しくは23時間56分4秒)
となり、一日につき約4分早く「ある恒星」-例えばオリオン座とか南中することになる。
真冬の夜、真南(南中)に見えたオリオン座。観測地点は半年後(365日÷2=約183日後)真夏になり、約12.2時間(183日✕4分=732分、
732分÷60分/時=12.2時間)早く南中する=南の空に出ていることになる。したがって、空は明るくてオリオン座を見ることができないわけ
である。(図-7で後ほど説明)
黄道・天の赤道・春分点・夏至点・秋分点・冬至点

図-6
地球は太陽を中心として半径約1.5億kmの円軌道(正確には楕円軌道)を公転している(図-6 黄色の小さい方の軌道)。
天球は半径無限大で作った球体であるから、地球の約1.5億kmの円軌は無視され、地球の公転軌道面=地球から見た太陽の軌道面、
地軸の向きなど面や軸の向き・角度が問題となる。
地球から見た太陽は天球上に投影される(図-6 破線で示している)。この天球の太陽の通り道を「黄道」、黄道を含む平面を「黄道面」、
太陽を通り黄道面に直角、かつ天球と交わる軸を「黄道の極」という。
地球の自転軸は黄道面に垂直ではない。地球の自転軸と黄道の極は23.4°をなしている。(図-6)そのため、天の赤道と黄道は一致しない。
地球は天の北極から「下」を見たとき(南極方向を見たとき)、反時計回りに公転している。天球上の太陽(黄道)が天の赤道を南から北へ横
切る点を「春分点」、最も北に寄った点が「夏至点」、天の赤道を北から南へ横切る点を「秋分点」、最も南に寄った点が「冬至点」。
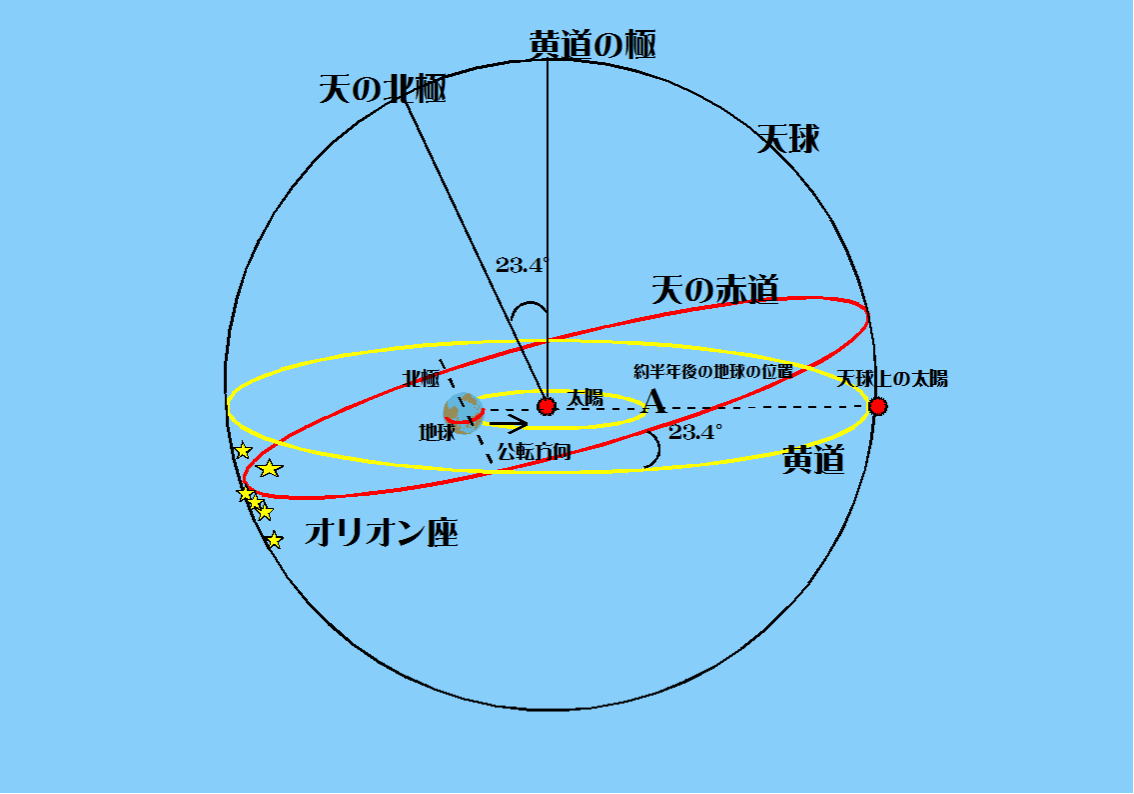
図-7
図-7において、天球上の太陽の位置(黄道上で)は冬至点にある。また、一方、オリオン座は天球上のおよそ180°離れた位置にある。
したがって、図-7の描かれた日は冬至で、真夜中にオリオン座が南中することになる。
半年後(365日÷2=約183日後)地球は公転し、図-7のAの位置に移動する。すると、Aの位置からは太陽(太陽は夏至点に位置する)とオリ
オン座が同じ方向に見える。全天で最も明るいのは太陽だから、オリオン座は夏には見えないことになる。
 宿 題 宿 題 
では①太陽が春分点にあるとき、②太陽が秋分点にあるとき、「オリオン座が南中するのはいつ頃か」、
図-7で考えることを宿題にしよう。
天球 練習問題 その 2
フランスのパリは北緯49°である。
夏至の日、冬至の日の太陽の南中高度は何度か?天球の図を描いて答えよ。
【解答・解説】
夏至の日の太陽の南中高度についてのみ解説、次のようになります。
天球の問題を不得意とする人は多いと思う。前の天球 練習問題 のように、必ず「図を書く」こと-。「この時は23.4°引くとか、足すとか、
足さない」とか、変なことを暗記するのは全くの無駄。
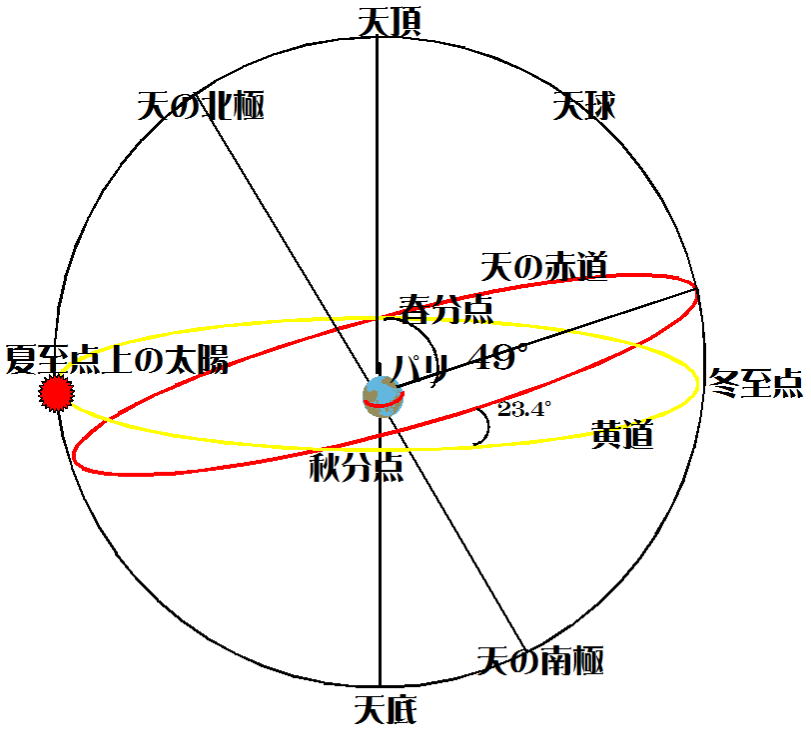
図-8
観測地点は北緯49°。図-2で、∠天の赤道-地心(=観測地点)-天頂は、観測地点の緯度(北緯)に等しくなる-だったので、
夏至点上にある太陽、パリの位置関係を「無限大の距離から」俯瞰すると図-8のようになる(図がやや不正確)。
ここで、また図-3のように順序に作図をする。
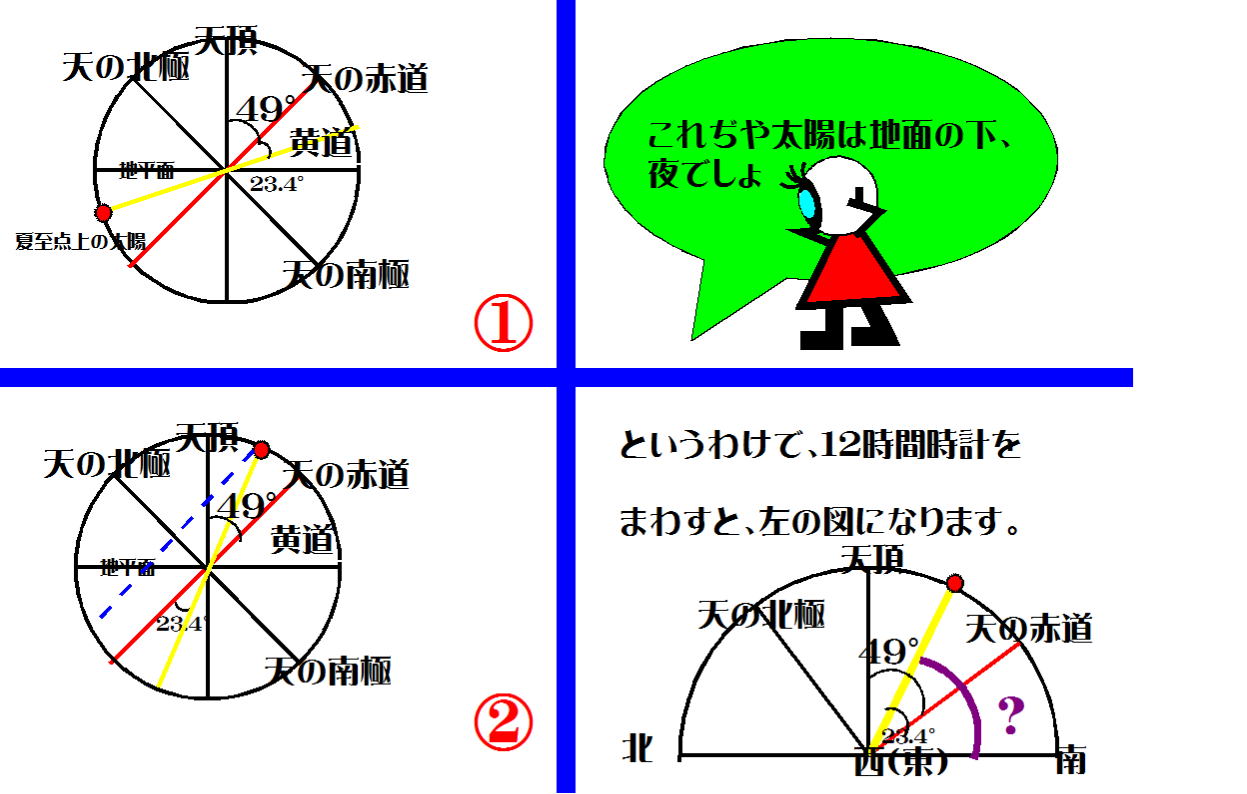
図-9
図-9①は図-8の天球の俯瞰図を、秋分点側から春分点側を真横に見た図になっている。
天頂と地平面とは90°で交わっている。図-9①では太陽は地平面の下にあるから、「夏至の日の夜」ということになり、
このままでは太陽の南中高度は図から求められない。
半日前(後)、太陽は天球の天の両極を軸として180°回転した図-9②に示される位置に来る。太陽は、天の両極、天頂を
通る大円上にあるので、南中している。
そこで図-9②右の図、半円の∠?について、図形的に計算して求めれば良い。
∠49°-23.4°=25.6° ∠25.6°+∠?=90°より、 ∠?=64.4°(答え)
または、
∠90°(天頂⊥地平面))-∠49°=41° 41°+ 23.4°=64.4°(答え)
同様に冬至の日の太陽の南中高度は何度か?図-9の天球を描いて考えて下さい。
案外、夏至の日の太陽の南中高度より求めやすいのでは?
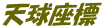
地球上の山や都市などの位置が緯度・経度の座標で示されるように、天球上での天体の位置を座標で示すのが天球座標。
二つの示し方がある。
① 地平座標
子午線と地平線(面)を基準にとして、「高度」と「方位角」で天体の位置を示す方法。
○高度(h):地平線(面)を0°、天頂を+90°、天底を-90°とする。
○方位角(A):南点(真南)を基準に西回り(時計回り)に、0°~360°とする。
○天頂距離(Z):天頂から観測している天体までの角距離で、天頂距離(Z)=90°-h
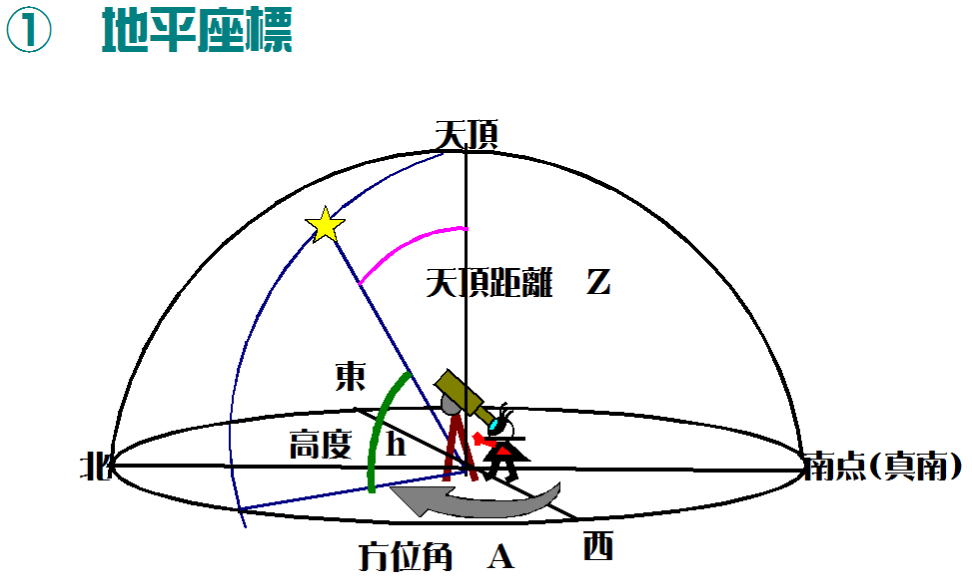
図-10
地平座標の特徴
○ 地平座標は次に説明する赤道座標(受験生はこれはクリアしなければなりません)より分かりやすい。
× 一つの天体について、地平座標は観測者の数だけあることになり、しかも天体の日周運動(=地球の自転)によって
座標が時々刻々変化する。
② 赤道座標
地球上の地点を緯度と経度で表示することと同じである。
緯度に対しては「赤緯」、経度に対しては「赤経」が対応する。
○赤緯(δ(デルタ)):天の赤道を0°、天の北極を+90°、天の南極を-90°とする。
○赤経(α(アルファ)):春分点(γ(ガンマ))を0h、角度15°を1hとして0h~24h(=360°÷15°/h)で表示する。
○時角(t):子午線と天の北極-天体-天の南極を通る大円のなす角で、子午線から天体方向に西回り(時計回り)に0h~24hで表す。(図-11)
図-11
赤道座標の特徴
○ 地球上の山や都市などの位置を緯度・経度で表示することと同じだから、観測地点が異なっても、また天体の日周運動によっても
「 赤緯・赤経」は変わらない。
×(△) 時角(t)は天体の日周運動によって大きくなる。(が、何ら問題にはならない)。ただ、地学選択者にとって理解しがたい。
  鋼製天球儀(渾天新図) 鋼製天球儀(渾天新図)
渋川春海作。1673年ころ。旧宮崎 延岡藩内藤家に伝来したと言う鋼製天球儀。 (上野 国立科学博物館にて)
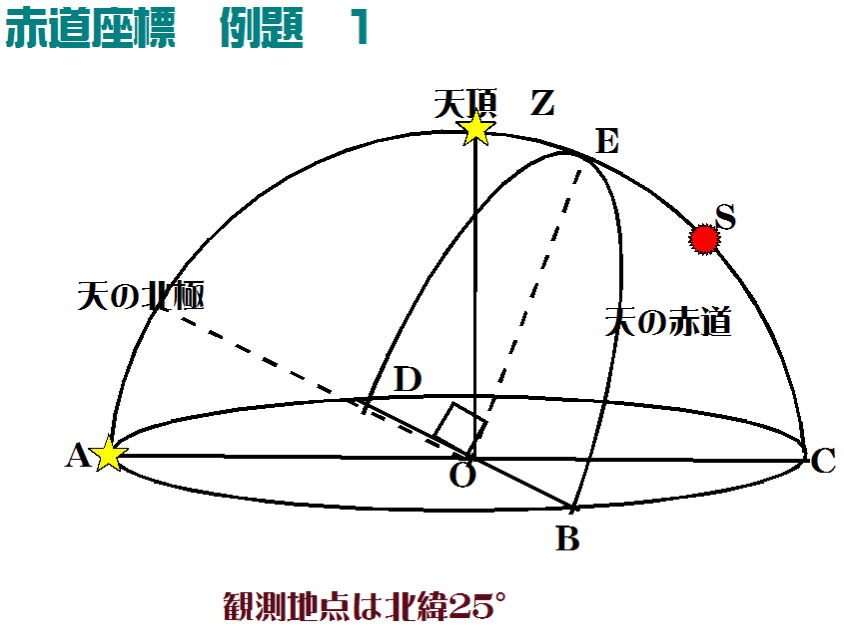
図は北緯25°の地点において様々な天体を観測した時の天球の半分を示している。以下の問いに答えよ。
問1 AC、BDが直交しているとする。B、Dの方位角は何度か。
問2 天頂Zにある恒星、およびAにある恒星の赤緯は何度か?
また、天頂Zにある恒星、およびAにある恒星の日周運動の軌跡を図中に描け。
問3 Sは冬至点にある太陽を示している。黄道を図示せよ。
問4 天頂Zにある恒星、およびAにある恒星の赤経を答えよ。
【解説・解答】
問1 弧A-Z-E-Cは天の北極・天頂・天の南極を通る大円だから子午線と見ることができる(図-2 参照)。
したがって、Cは南点(真南)、Bは西,Aは北、Dは東となる。
地平座標では方位角は南点(真南)を基準に西回り(時計回り)に角度を測ることになっている(図-10 参照)。
答え Bの方位角:90°、Dの方位角:270°
問2 図-1、2、3②の説明より、天頂方向と天の赤道のなす角は観測地点の緯度に等しい。
一方、∠AOE'は∠EOCの対角となる。下図参照
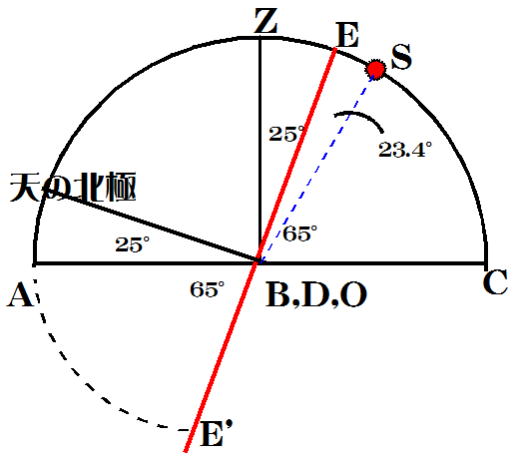
答え Zの赤緯:+25° Aの赤緯:+65°
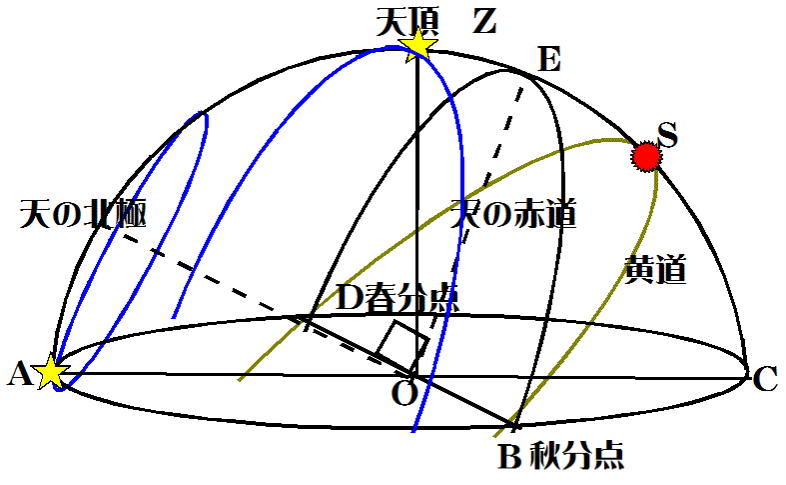
答え 恒星A、Zの日周運動の軌跡は下図のとおり
天球は天の北極、天の南極を通る軸を中心に回転。天球に張り付いた天体は円運動を行う。下図参照
問3 下図参照
問4 赤経は春分点を基準にし、東回り(反時計回り)に角度15°を1hで表す決まりであった(図-11)。
上図のように、D点が春分点と決まったから、天の北極の真上から恒星Z、Aを眺めたら、天球上でどのようになるか、
図示してみる(下図参照)。
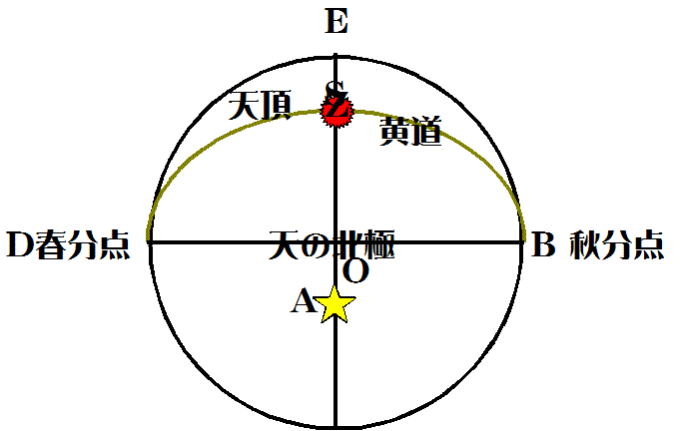
答え 天頂Zにある恒星の赤経:18h、Aにある恒星の赤経:6h
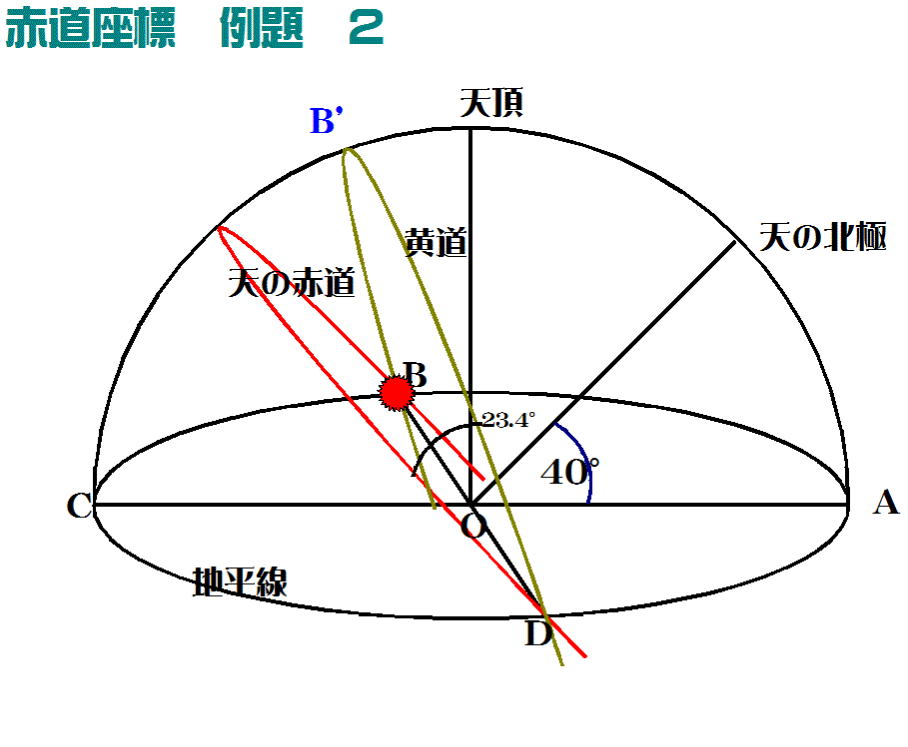
上図は北緯40°において地平線にかかる太陽(赤丸)を示している。直線ACとBDは直交し、天頂方向と
地平面も90°で交わっているものとする。
以下の問いに答えよ。
問1 A、B、C、Dと太陽の位置(方位角)を地平座標で示せ。
問2 Bは黄道・天の赤道が交わる点で、太陽が位置している。
①Bは春分点か秋分点か?
②太陽の天球座標の位置を地平座標、赤道座標で表せ。
問3 この日太陽の南中高度は何度か。
問4 3ヶ月後の太陽の位置を赤道座標で表せ。また、南中高度は何度になるか。
【解説・解答】
問1 弧 A-天の北極-天頂-Cは子午線。(図-2 参照)。
したがってAの方位は北。B=西、C=南、D=東。
答え A=180°、B=90°、C=0°、D=270°、太陽=90°
問2 ①天の北極側から見たとき、太陽は黄道上を東回り(反時計回り)に年周運動する(図-11)。
問題文の図では、太陽は天の赤道を天球の南から北側に横切ろうとする位置=Bにあるから、太陽は春分点
にある。春分の日の日没を表した図である。
②太陽の位置の赤道座標は、春分点にあるので、赤緯0°、赤経0h
太陽の位置の地平座標は問1のBのそれと同じ。90°
答え ①春分点 ②太陽の位置の赤道座標 赤緯0°、赤経0h、 地平座標 90°
問3 この日太陽は春分点、天の赤道上にある。太陽の日周運動は天の北極・南極を軸とした回転によって、
南中時太陽は下図の位置となる。
太陽の南中高度=90°-40°=50°
答え 50°
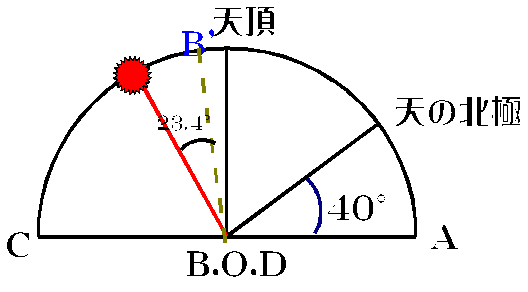
問4 3ヶ月後の太陽の赤経は、1°/日✕90日=90°、90°÷15°/h=6h。一方赤緯は夏至点上に太陽が
来るので、+23.4°
答え 赤経6h、赤緯+23.4°
赤経で表すより、角度にして90°黄道上を移動し夏至点に位置する-と行ったほうが理解しやすい-はず。
3ヶ月後太陽は、上図及び下図ののB'点に位置する。
問3で∠太陽-O-C=50°と分かっている。
したがって南中高度=∠B'-O-C=50°+23.4°=73.4°
答え 73.4°
|
|
|
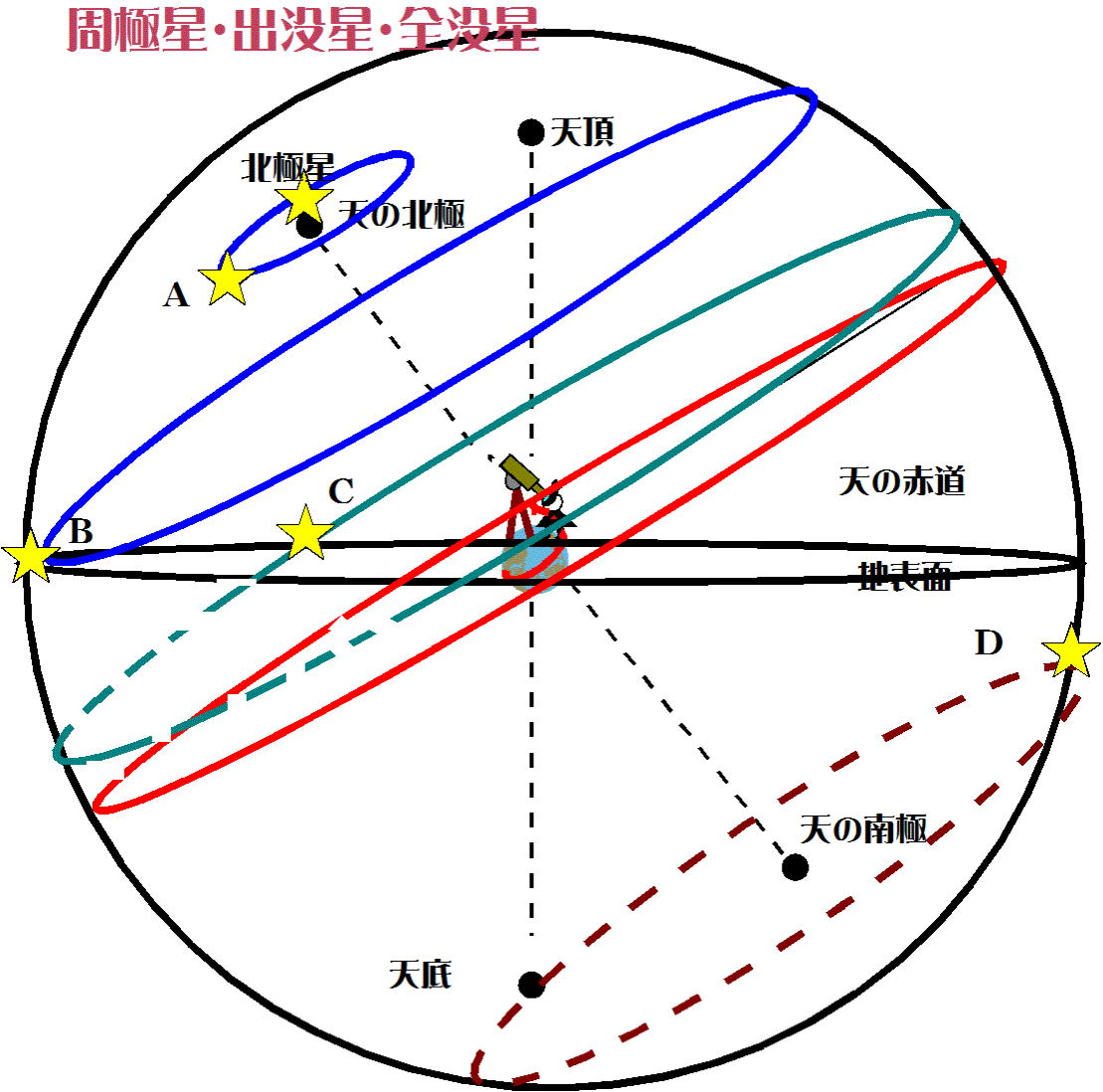
図-12
図-1、赤道座標例題1【解説・解答】の2つめの図から気がついている、あるいは元々知っている人が
いるかもしれない。地面に没しない星があったり、空に見えている星が地面に没する星が
あり、それらが観測地点の緯度と赤緯に関係がありそうだな-ということを。
例えば図-12で、ひとみちゃんが望遠鏡で北極星と恒星Aを観測したとする。
この日何かの加減(?・・・)で夜が24時間続いたとすると、ひとみちゃんは下図のような観測をするはずである。
(北極星は、天の北極から角度にして約0.7°ずれていて、天の北極にピッタリに位置してはいない)

上の図から分かるように、恒星Aは日周運動によって地平面の下に隠れることはない。このような恒
星を、極を周(めぐ)る星ということで「周極星」という。図-12では恒星Bはぎりぎり周極星である。
恒星Cは北東の地平線から登り南中し、北西の地平線に没する。つまり空に出たり地平線(
面)の下に没したりするので「出没星」となる。
一方、恒星Dは日周運動によって地平面より上に出ることはない。図-12で示された観測地点
にいるひとみちゃんは恒星Dを見ることはできない。地平面より上に現れない星であるので「全没星」。
では「周極星」、「出没星」、「全没星」となる恒星と観測地点とどのような関係があるだろう。
図-12で、仮にひとみちゃんが北緯30°で観測していたとしよう。
図-1、2、3と図-12より、図-13を描くことができる。
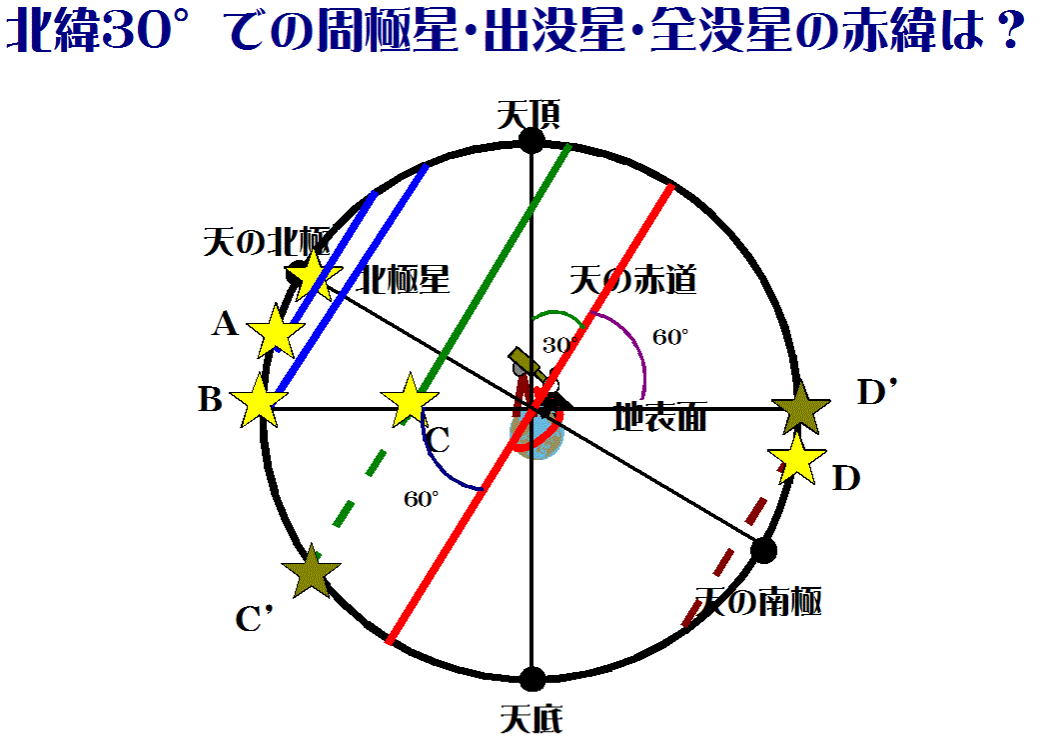
図-13
「周極星」
図-13・観測地点の北緯は30°で、恒星A、Bは周極星。恒星Bより天の北極側にある
恒星は周極星となることが分かる。
では、恒星Bの赤緯は? 図-13より+60°と分かる。
すなわち、観測地点の緯度をθ、周極星であるための赤緯をδとすると
δ≧(90°- θ)
「全没星」
図-12で恒星Dは「明らかな」全没星。恒星D'が仮にあったとすると、ぎりぎり全没星で、恒星D'から
天の南極の間にある恒星は、北緯30°において観測されることはない。
恒星D'の赤緯は-60°、天の南極にある星は-90°。北緯30°において、赤緯が-60°から-90°
の恒星は観測できないことになる。
すなわち、観測地点の緯度をθ、全没星であるための赤緯をδとすると
δ≦-(90°- θ)
「出没星」
天球上の恒星が、恒星D'より天の赤道側に、また恒星Bより天の赤道側にあれば出没星となる。
赤緯は-(90°- θ)から90°- θの範囲ということになる。
すなわち、観測地点の緯度をθ、出没星であるための赤緯をδとすると
-(90°- θ)<δ<(90°- θ)
南十字星の「十字」の北(上)の星の赤緯は-58°、「十字」の南(下)の星の赤緯は-63°。図-13の
恒星D'の赤緯(-60°)より大きいので、計算上では北緯30°の地点で南十字星の北の星を見ることができる-
が「十字」に見えないから、何が何だか分からない。。
北緯26°付近(八重山列島の南)まで南下しないと南十字星の全体を実際は見ることができない。

 例題 南十字星(全体の赤緯:-63°)が周極星として観測される緯度の範囲を答えよ。 例題 南十字星(全体の赤緯:-63°)が周極星として観測される緯度の範囲を答えよ。
① 南十字星の赤緯が-63°だから天の南極を周る周極星。
したがって、天の南極が地表面上に出ていなければならない。(図-A)
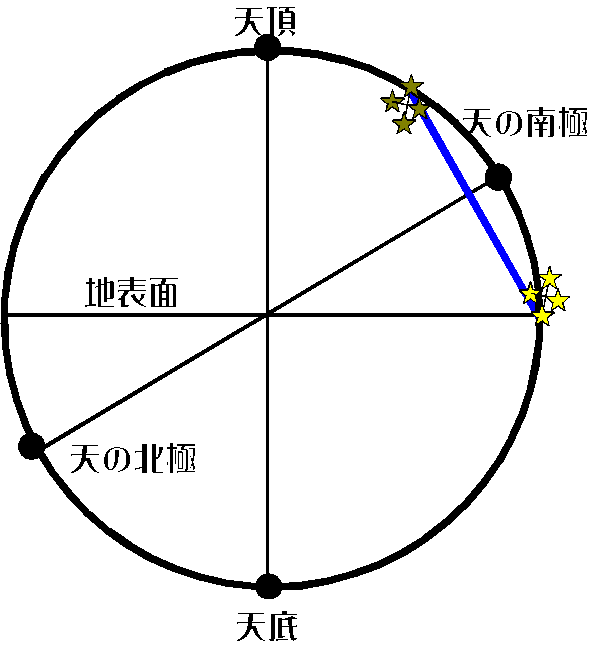 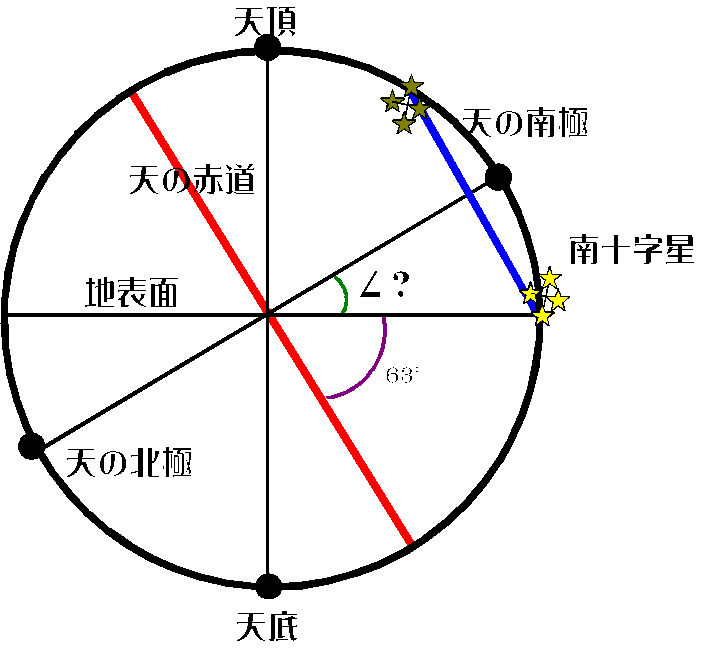
図-A 図-B
② 南十字星から天の北極に63°向かったところに天の赤道があるから図-Bとなる。
天の両極と天の赤道は90°で交わる。したがって∠?=27°
天の南極の地平からの高度は南緯に等しいから南緯27°より高緯度で南十字星は周極星になる。
答え 南緯27°~90°
③図-Cは南極上で観測した場合で、全天の恒星が円を描くように日周運動を行う。 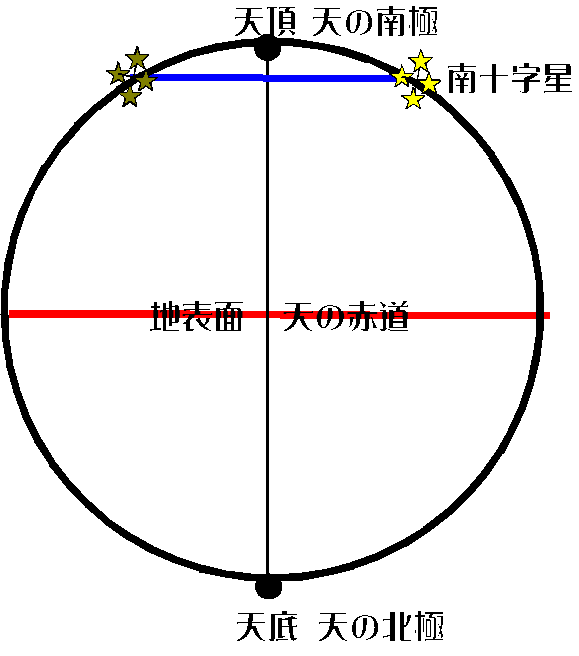 図-C 図-C
|
|
|
|
|
|
|
|
|
|
|
|


