  

教科書でよく説明に持ち出されるのは、「風がなく地面に垂直に雨が降っている。電車に乗っている人が
電車が動き出すと、真っ直ぐに降っている雨が斜め前方から降っているように見える」、「これと同じように、
真上からさす恒星の光を観測するのに望遠鏡をある角度だけ傾けなければならない」そのずれの角度が光行
差で、一「年」を「周」って観測されるのが「年周光行差」-ですと。
ここでは、電車に乗らず雨の中歩く(結構速いスピードで)ことで光行差を考える。
|
 図-1 図-1 |

|
図-1では雨は
地面に対して垂直
に降っていて、観
測者は停止した
ままの様子が描か
れている。
傘を斜めにさす
必要はもちろんな
い(図-1)。 |

図-2
|
ところが観測者がある速度で移動すると、雨が地面に垂直に
降っているにも拘わらず、運動が合成され傘をある角度だけ傾
ける必要がある。この場合、観測者の移動方向と雨の降ってく
る方向が直交していること-ここに注意を払っておきたい(図
-2)。
では雨の降って来る方向に歩いて行く-ことは出来ないので、
雨の中傘をさしロケットに乗っていくことにする(図-3)。
雨の降って来る方向とロケットの進行方向=観測者の移動方
向は一致、平行である。この場合、傘を傾ける必要が無いのは
ご覧のとおりである。
図-2、図-3から傘を傾ける必要がある(か、無いか)
(光行差)は、雨の降って来る方向(恒星の方向)と観測者
の移動方向(地球の公転)が大きく関係していることに気
づく。
|

図-3 |



上の雨の中の佇み、歩行の話から地球の公転についての話
に移る。
図-4のように、地球が静止している場合、ある星を観測すれ
ば、望遠鏡を傾ける必要はない。
図-3を見て、「地球が観測している星に向かって直進してい
く場合もあるじゃないか」という人もいるかもしれない。
救急車が近づいてくるとき「ピーポーピーポー」の音の「高さ」
(大きさではない)が次第に高くなること(ドップラー効果)を経験
しているはず。もしも地球が観測している星に向かって直進して
いく場合があれば、救急車の音と同じように、星の色が変化して
観測されるので地球の運動が確認される。
一方、図-5のように星を観測するのに望遠鏡をある角度だけ
傾けなければならないのは、図-2で見た雨の中での歩行と同
じように、地球が移動(公転)しているためである。光行差は地球
公転の証拠となる。
|
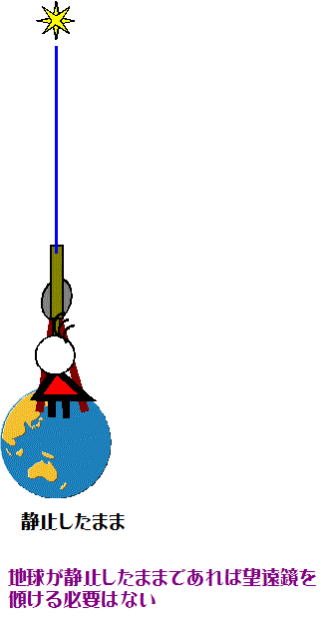 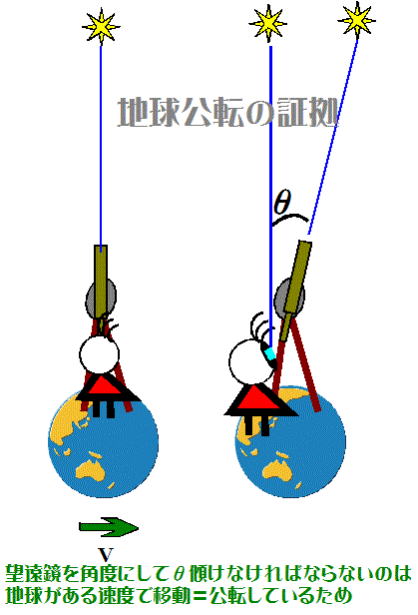
図-4 図-5 |
 
|
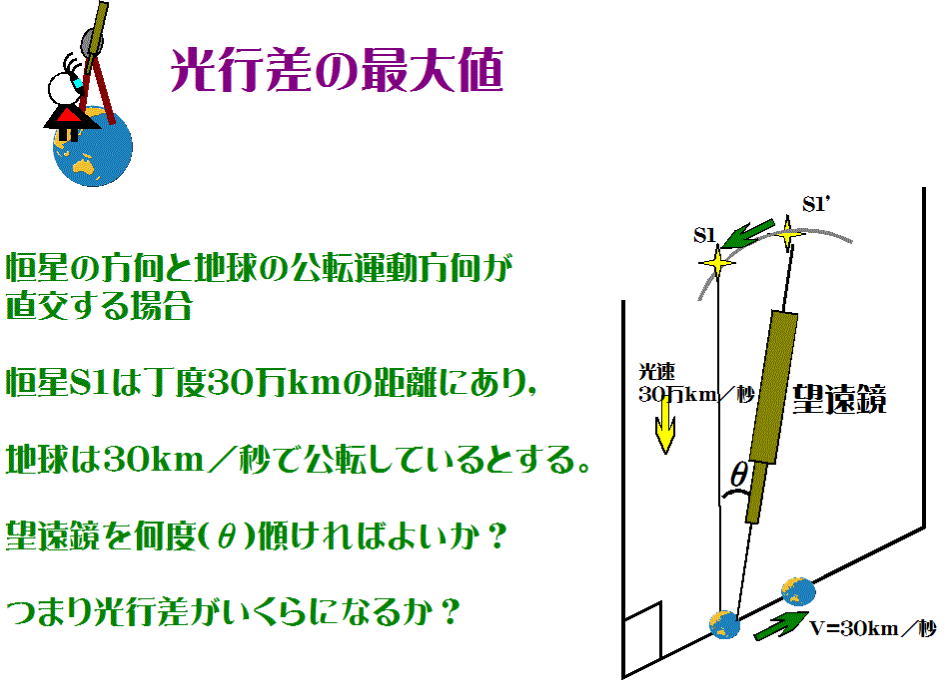
図-6
|
時間を1秒に限る。
まず、図-6の扇形S1・S1'・地球に着目する。時間が1秒であるので、扇形の半径は30万km、
弧S1S1'は地球の公転に伴う見かけの運動で30kmと近似的に見ることが出来る。
扇形S1・S1'・地球と半径30万kmで描いた円(周)について、
弧S1S1':中心角θ=半径30万kmで描いた円周:360°
極めて小さいことが予想されるので、角度の「度」の単位を「秒」単位に変換しておく。
30km:中心角θ=2✕3.14✕30万km:360✕60(分)✕60秒
中心角θ=30km✕3.6✕102 ✕3.6✕103 秒÷2✕3.14✕3✕105km
=20.6秒-年周光行差の最大値
(上の計算には大雑把な値を用いているため、教科書の20.5秒と異なります。
詳しくは図-8以降で説明)
しかし、「恒星からやってくる光の方向と、地球の公転運動の方向が直交する」ばかりある
わけではなく、それはまして稀であり、恒星からやってくる光の方向と地球の公転運動の方向
とは任意な角度となる場合が多いはずである。
そこで地球の進行方向の斜め前方、斜め後方に恒星がある場合、地球の軌道方向(運動方向)
と恒星の光の差す方向とのなす角度と関係と年周光行差がどのような関係になっているか考えて見よう。
 
|
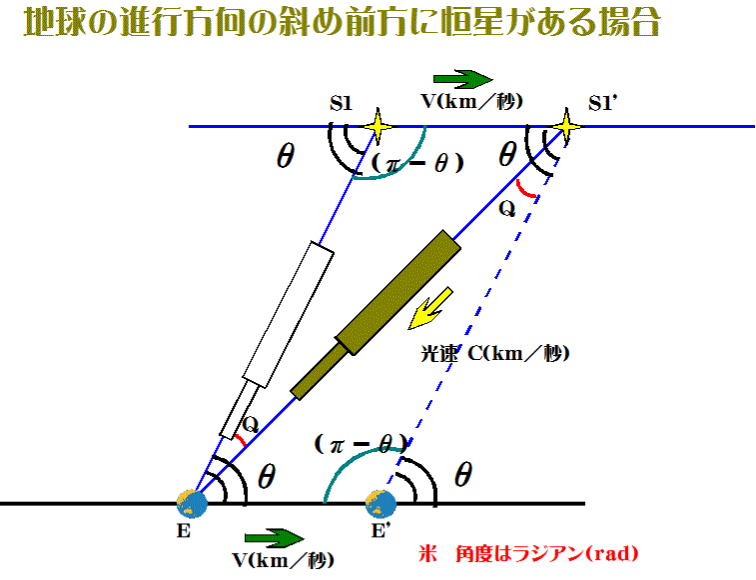
図-7
|
弧度法(ラジアン(rad))
これまで角度を「度」で表す方法であった。扇形の弧の長さは中心角に比例する
ことを利用したのが弧度法。
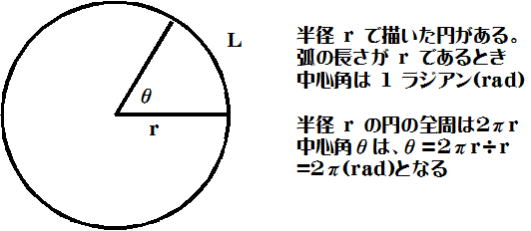
図-6と同じように時間を1秒に限って考える。恒星S1が地球の進行方向に対し
前方θ(rad)に位置している。地球はV(km/秒)で運動(公転)している。
もし地球が停止していれば白色の望遠鏡で恒星S1を観測できる。しかし地球は公転
しているため、見かけ上恒星はS1'へ遠のくように見え、望遠鏡を∠Qだけ傾ける必要がある。
停まっている電車の窓から、斜めに雨が降っていたのが、電車が一定の速さで走ってい
ると横殴りの雨に見えることと同じである。
図-7の△S1・S1’・Eにおいて、正弦定理を用いると
|
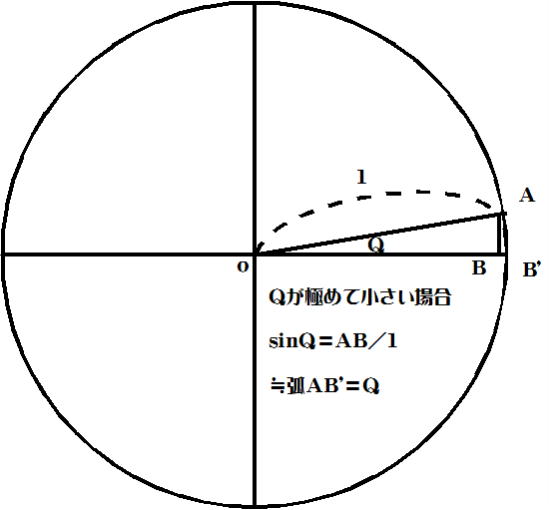
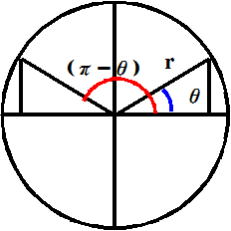
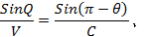 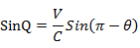 Qが極めて小 Qが極めて小
さいと き 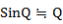 として良いので(右図参照) また、 として良いので(右図参照) また、
Sin(π-θ)=Sinθ
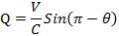 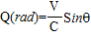 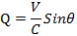
|
  |
 
|
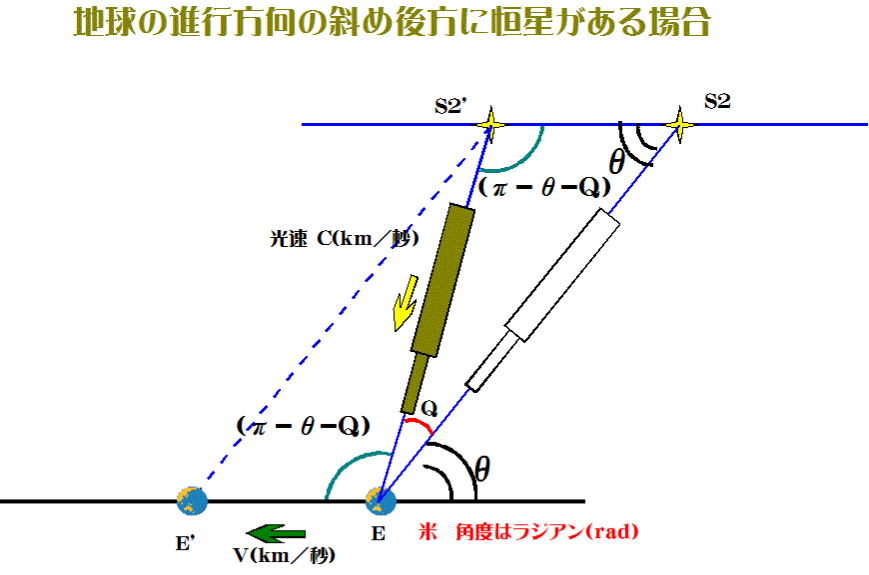
図-8
|
この場合は地球が停止していれば白の望遠鏡で恒星S2を観測できる。が、地球が
E'へ移動することにより恒星はS2'の位置に追いついて来たように見える。そのため望遠
鏡を角度にしてQだけ起こさなければならなくなる。
図-8の△S2・S2’・Eにおいて、正弦定理を用いると
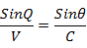 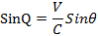
図-7と同様に
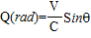 |
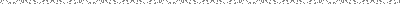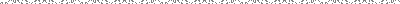
ということで、2つの場合に分けて考えても望遠鏡を傾けなくてはならない角度Qは、地球の軌道方向(運動方向)と恒星の光の
差す方向とのなす角度θに規制されていることが分かる。
Qの最大値は、Sin90°=1のとき最大となり、V(地球の公転速度)をC(光速)で割った値で一定である。では、その詳しい値は
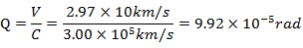
Qの値はラジアンなので、これを角度の「秒」単位に換算する。
180°=π(rad)、 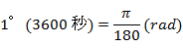
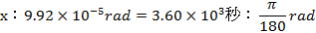 xについて解いて、 xについて解いて、
20.47秒≑20.5秒・・・年周光行差の最大値
|
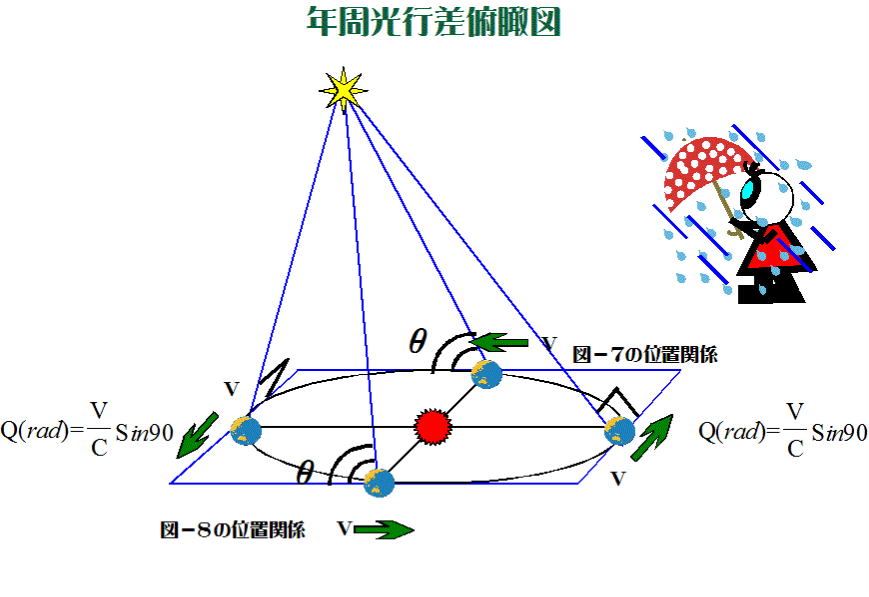
図-9
|
図-9の左右の 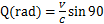 の位置関係と得られた年周光行差の最大値 の位置関係と得られた年周光行差の最大値
「20.47秒≑20.5秒」は、図-6の説明とその値に一致するものとなる。
図-9から分かるように、1つの恒星について、光行差は1年を周期として、20.5秒 ~
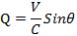 ~20.5秒~ ~20.5秒~ 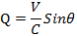 ~20.5秒と変化することになる。 ~20.5秒と変化することになる。
これは地球が、太陽を1つの焦点とするほとんど円に近い楕円軌道を公転している
ことに由来する現象であり、
年周光行差の最大値は20.5秒と大きく、年周視差の発見よりも早く、1727年、イギリスの
ブラッドレー(James Bradley)によって報告された。
|

視差とは、ある物体を離れた場所から見たときの、視線方
向の違い。
年周視差は、
「比較的地球に近い天体から地球軌道の半径を見込む角
度」で0.01杪(角度)が限界。フリードリッヒ・ウイルヘルム・
ベッセル(Friedrich Wilhelm Bessel,(ドイツの数学者、天文
学者) )が1838年、年周視差を発見。
年周視差の角度は極めて小さく、年周光行差の測定よりも
遅れて発見・測定された。
例えば、目の前にコーヒーカップがあるとして左の眼で見た
ときと、右の眼で見たときではコーヒーカップの見え方が異なっ
ている。これは、左の眼と右の眼とがある
距離だけ離れていることとコーヒーカップが比較的近い距離
に置かれているからである。
もし、視力が良くて10kmも先に置かれたコーヒーカップが見
えるようであれば、視線方向は交差することなく平行のまま、視
差はなくなるだろう。
地球と恒星の関係で視差を考えると次のようになる。最も地球
に近い恒星は4.3光年(光の速さで4.3年かかる距離にある-とい
うこと。太陽までは8分19秒ほどと近い。)もあれば、30億光年の
距離にある銀河もある。先の、左の眼と右の眼に当たるのは、地
球の公転軌道の両端に位置したときの地球。4.3光年の距離にあ
る恒星視線方向は1年を周期に変化して見えることなる。
|
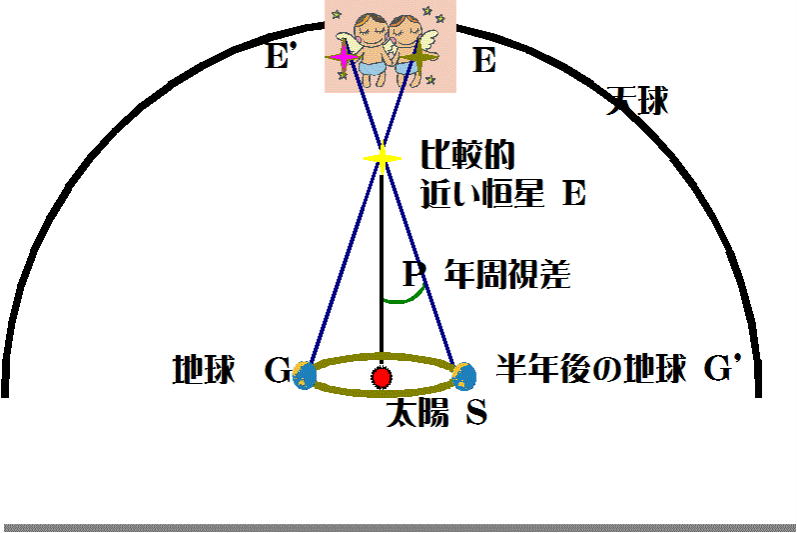
図-10
年周視差(図-10)の説明
地球がGの位置にあったとき、比較的近い恒星Eは遠い星座(図-10では双子座の
絵になっている)のEの位置にあるように見える。
地球は公転運動を行い、半年後にはG'の位置に来る。すると恒星Eを観測すると今度は
遠い星座のE'の位置にあるように見える。
このように、地球(太陽(天球は半径無限大で考えられているから、太陽-地球間の距
離は図に表せないほど小さい))に近い恒星の見かけの位置が、一「年」を「周(めぐ)」って
変化する。
とくに図-10の比較的近い恒星Eは、黄道の極(27 天球 図-6,図-7)に含まれて
いるため、天球上では円を描くように観察される。
|

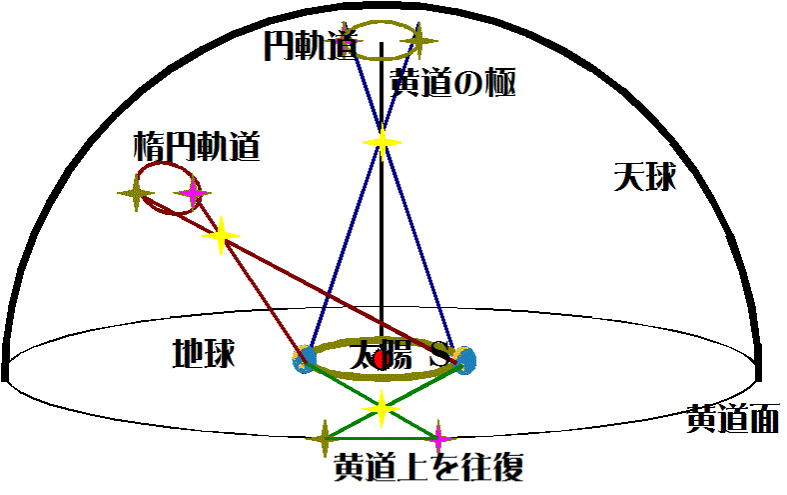
図-11
|
① 黄道の極に含まれる恒星
図-10で説明したように黄道を中心に円軌道を描くように見える。
② 黄道の極及び黄道面に含まれない恒星
図-11、左に示されるように、天球上では楕円を軌道を描くように見える。
③ 黄道面に含まれる恒星
1年を周期に黄道上を往復運動するように見える。 |
年周視差(p(杪))が測定できれば、その恒星の距離(d)が光年
の単位で求められる。
公式 d=3.26/P
上の公式が如何に導かれるか説明を行いますが、絶対
理解しなければならない事項ではありません。数字が大きく
なるだけで、原理は簡単です。
当HP、No.1 地球の大きさを測る エラトステネスの方
法、「扇形の弧の長さは、中心角に比例する」を思い出し
ていただきたい。
図-12に恒星、太陽、地球が描かれている。本来OSEは
直角三角形(∠ESO=90°)、ES=1.5✕108kmである。ここで、
太陽SをS'まで、つまりOEを半径として描いた円弧上に移動させ
てもOS'≓OS≓d、ES=ES'(=1.5✕108km)として差し支えはない。
(S~S'の距離は、何光年も離れた恒星Oからすれば無視できる
長さであるから)
ここで半径dで描かれた扇形(OES')と円に着目する。
①扇形(OES')において
弧'ES'(=1.5✕108km)、にたいして中心角はP(杪)
②一方、半径dで描いた円において
円の全周 2πd、にたいして中心角は360°(✕60(分)✕
60(杪))
先のエラトステネスの方法、「扇形の弧の長さは、中心角に
比例する」ので
弧'ES'(=1.5✕108km):P(杪)=円の全周2πd:360✕60✕60(杪)
2πd P =1.5✕108 ✕ 3.6✕102 ✕3.6✕ 103
d =1.5✕108 ✕ 3.6✕102 ✕3.6✕ 103 ÷6.28p=1.5✕ 3.62✕
1013 ÷6.28p
=19.44 ✕ 1013 ÷6.28p=3.09✕ 1013 km÷p
3.09✕ 1013 kmを光年単位に変換するので、
光速は3✕ 105 km/杪、1年は365(日)✕24(時間)✕60(分)✕60杪
=3.15✕ 107 杪、したがって光は1年間に3✕ 105 km/杪✕3.15
✕ 107 杪=9.46 ✕ 1012 km 進むこととなり、
1光年の距離=9.46 ✕ 1012 km
3.09✕ 1013 kmを 9.46 ✕ 1012 km/光年で割って、
3.09✕ 1013 km=3.26光年
すなわち d =3.09✕ 1013 km÷p=3.26÷p(光年)
年周視差が1秒(second)の時、dは3.26光年の距離となる。
そこで、3.26光年あたりの距離を1パーセカンド(1/second)とし、
1PC(1PSではない)=1パーセクという単位で表す。
|
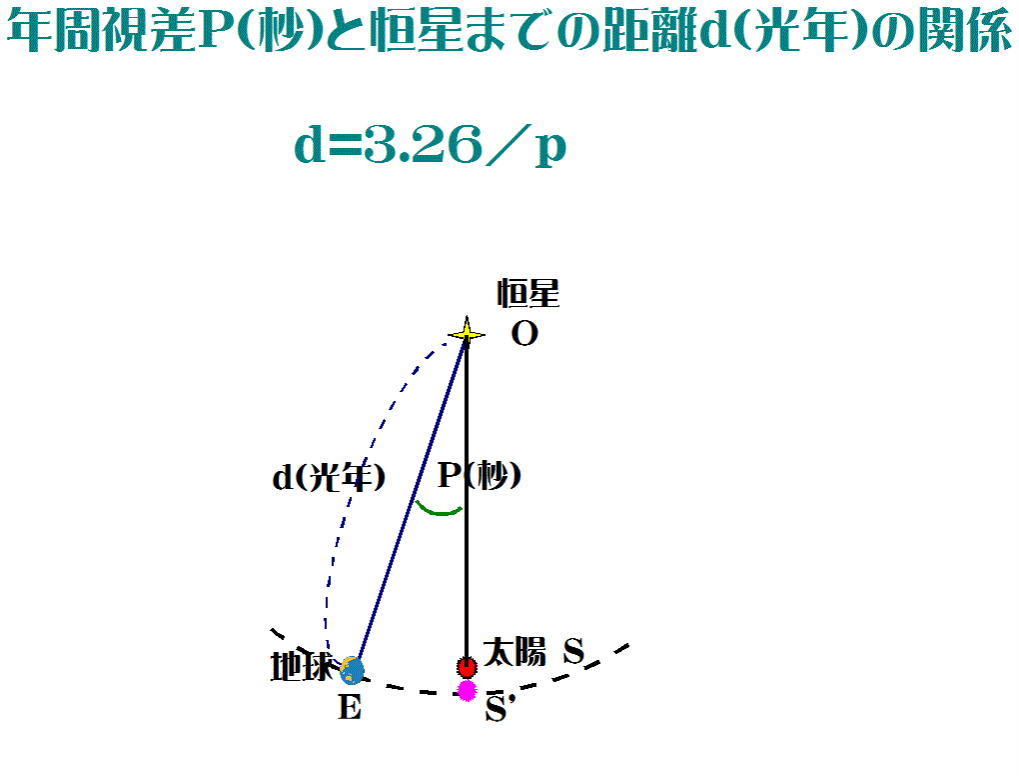
図-12
|
公式 d=3.26/P(光年)=1/P(1パーセク(1PC))
例題
シリウス(おおいぬ座α星)(冬の季節に見られるオリオン座。三つ星が並んであります
が、三つ連なった 星を東に延長していくとひときわ明るく輝く星)の年周視
差Pは0.379秒。
シリウスの距離は何光年か、何PCか?(有効数字3桁)
【解答】
d=3.26/P=3.26/0.379=8.60光年
d=1/P=1/0.379=2.64PC |
|
|
|
|
|
|
|
|




|


