
惑星の説明に、当HP No.26 惑星で「人を惑わす星」として説明を行
った。
一方「恒星」の「恒」は「いつも変わらない」、「久しく一定している」の意で
あり、「恒星」は天球上に張り付いて「動かない」星と言う意味から名付
けられた経緯がある。
大昔の人は夜空を観察して、「恒星」の中を移動し、次第に位置を変
える星の存在=「惑星」に気づいた。
|
惑星の視運動
| 順行 |
天球上を太陽の年周運動と同じように西から東へ移動するように見える |
| 逆行 |
天球上を東から西へ |
| 留 |
天球上に惑星が留まっているように見える。順行から逆行、逆行から順行へ変換する際。 |
|
|


2006年冥王星は「準惑星」に格下げになったものの、それを含め、また
ほとんどの惑星は太陽の公転軌道面付近、つまり黄道付近に観察され
る。
したがって、太陽に近い位置にあるときは全天で最も明るい太陽のた
めに観察出来ない。

もしも「留」や「逆行」が実際起きたら、「留」の時には一瞬公転運動が
止まり太陽の引力だけが地球に加わり、太陽に向かって落下をは
じめる。「逆行」が開始すれば季節が戻ったり、また「順行」に戻れ
ば季節が重複したり、1年の長さが変化したり大変なことになる
・・・。
「逆行」するように見えることが起きるのは、各惑星の公転速度
(km/秒)が等しく一定ではなく、太陽に近い惑星ほど大きく(速く)
遠くなるほど小さく(遅く)なっているためである。
 |


惑星の視運動で、逆行といっても、ある日突然、ある惑星の公転運動
の方向が反対になり「逆行」するのではないことは、文系の皆さんでもお
分かりですよね。
地球は水星・金星から見れば「外惑星」で、ある時「逆行」しているし、一
方火星や木星からすれば「内惑星」ではやり、あるとき「逆行」している。こ
のような事は実際の生活に支障を来さないので、わざわざ天気予報のよ
うに「留予報」、「逆行予報」、「順行予報」などしない。

前に説明したように太陽の引力は、太陽と惑星の質量の積に
比例すとともに太陽~惑星間の距離の二乗に反比例する。この引
力と個々の惑星の公転の遠心力が釣り合っているため、太陽に引か
れ近づくことも離れることもなく円運動(正確には楕円運動)を行って
いる。太陽に近い惑星ほど大きな(強い)引力を受けるため、公転速度
は大きい(速い)。
|
図-1は外惑星(およそ火星を意識して作図)の順行・逆行を概念的
に表している。約37日ごとに地球と外惑星の位置関係を1~11で表し、
地球から見た外惑星が天球上にどの位置に見えるか図示している。
図-2は、ひとみちゃんが黄道面に平行に立ち、太陽のまぶしさにも
めげずに外惑星の視運動を確認できたとして、順行・逆行・順行の様子
を図示している。(この場合、順行・逆行・順行の動きは黄道上で往復運
動になり、図-2のようなS字にはなりません。説明のための概念図で
す。)

図-2
(外惑星の軌道傾斜は無視し、順行・逆行を概念図として表したものです。) |
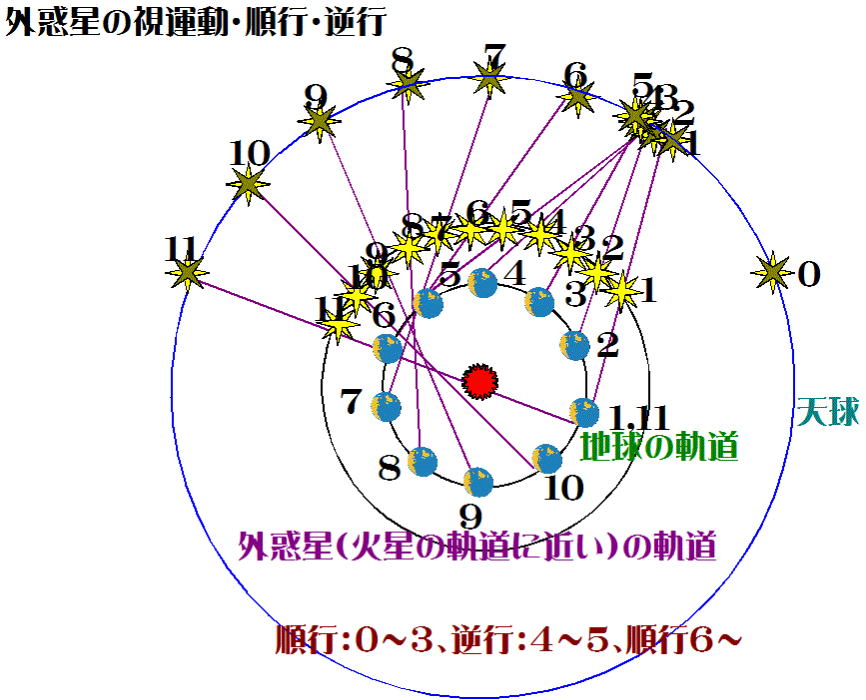
図-1 
|
内惑星の順行・逆行については、図-3、4に表している。外惑
星と同じように、内惑星と地球のある位置関係で逆行現象が起こ
る。

合(ごう)、衝(しょう)は、太陽・地球・外惑星の位置関係を表す言葉。
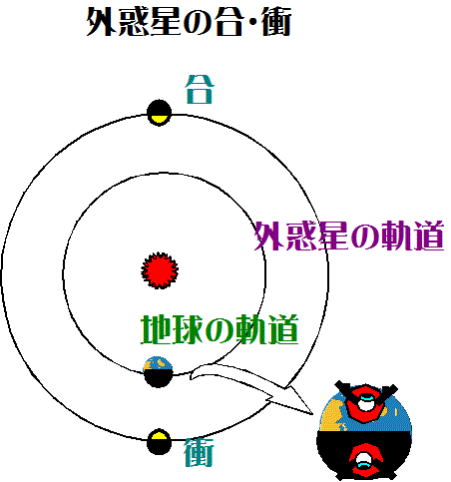
図-4
|
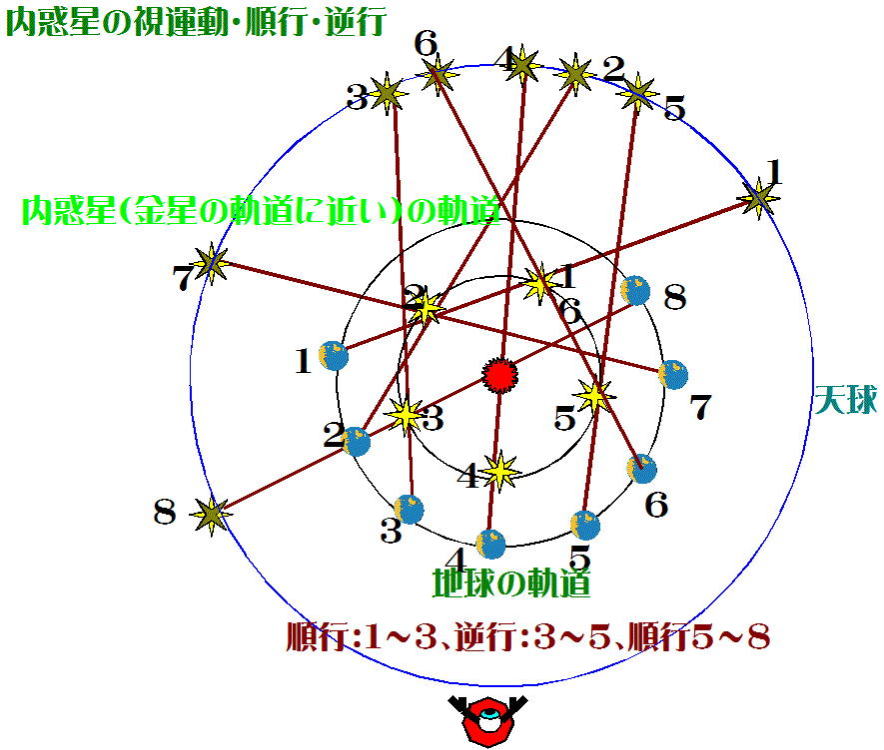

図-3 |
合:地球-太陽-外惑星の順で一直線に並んだ時。
この時、外惑星は太陽と同じ方向にあり、観測できない(図-4)。
衝:太陽-地球-外惑星の順で一直線に並んだ時(図-4)。
この時、外惑星は太陽と180度離れており、時間にして12時間遅れの運動を行う。
つまり太陽が西の地平線に沈むとき、外惑星は東の地平線から登り、真夜中に南中
する。地球に最も近くにあり(したがって大きく観測され)、一晩中観測できることになる。
図-1,2から分かるように、外惑星が衝付近にあるとき逆行現象が起こる。
なお、同じ位置で合・衝が起こることはない。地球、外惑星の公転速度がそれぞれ異な
るからである。(次の「会合周期」の項で説明)
|

|
図-5を見て分かるように、内惑星は、太陽-地球-内惑星の順に
並ぶような「衝」の位置関係はとり得ない。内惑星であるから、太陽の
近傍を公転しているためで、地球から観測した際に、「最大である角度
だけ太陽から離れること」が可能となる。この角度を「最大離角」という。
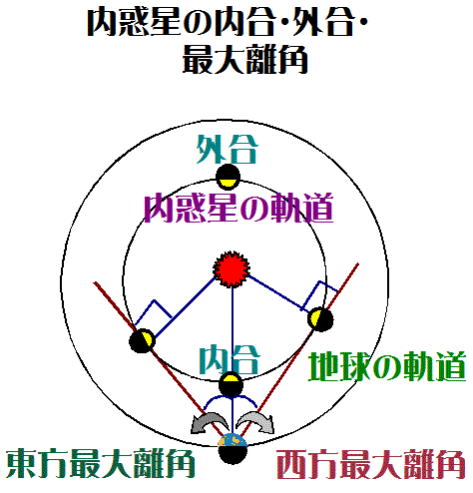
図-5 |
a 西方最大離角
地球から内惑星の軌道に引いた接線の接点に内惑星が位置したと
き、内惑星が太陽から最も遠く離れて見えることになる。この時、内惑星
が太陽より西にあるとき、この∠太陽-地球-内惑星のなす角を西方最
大離角という(図-5、6)。
図-6 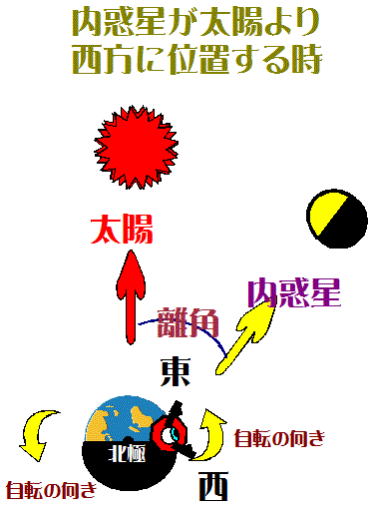
|
内惑星が西方最大離角(近く)の位置にあるとき、どのように観察されるだろう?
図-6は、図-5の下の部分、西方最大離角の部分を拡大して描いている。天の北極側から見て、ひとみちゃんは夜明けにならんとするところ
にいる。
つまり内惑星が西方最大離角(近く)の位置にあるとき、夜明け近くになると内惑星が東の地平線から上がってきて、次第に空が明るくなり続いて
太陽が昇ってきて内惑星は(太陽の明るさのために)見えなくなる。
金星は地球に近く大きく見え、太陽からの離角が大きく「明けの明星」と名付けられる。が、金星・地球の位置関係によるので、「明けの明星」を
一年中毎日見ることが出来るわけではない。
|
b 東方最大離角
内惑星が東方最大離角(近く)の位置にあるときは、図-6での内惑星、太陽が互いに反対の位置関係になる。
この場合は、全天で最も明るい太陽が西の地平線に沈んだ頃、内惑星は西の空に輝く。つまり「宵の明星」である。
内惑星には水星、金星の2つがある。惑星の軌道は太陽を中心とした円軌道ではなく、太陽を1つの焦点とした楕円軌道であるので、それぞれの
惑星の離角は一定ではない。水星の最大離角は18.1°~28°、金星は45°~47°ほどである。
|

|
あるとき太陽-地球-惑星がある位置関係をとり、再び太陽-地球-惑星が同じ位置関係をとるまでの時間(期間)-
を会合周期。
例えば、外惑星で言えば、あるとき衝になり、次に衝になるまでの時間。また、内惑星であれば、あるとき内合になり、次に内合
になるまでの時間-ということ。
前に、「惑星の視運動」の項で説明したように、太陽に近い惑星ほど速い速度で公転している。
「会合」のイメージは、陸上競技場で内惑星が内合、地球、外惑星が衝で一斉にスタートしたものの、 内惑星、地球、外惑星の
走るスピードが異なるため、何周遅れかで再び内惑星と地球が並んだり(内合)、地球と外惑星が並んだり(衝)する関係に似ている。
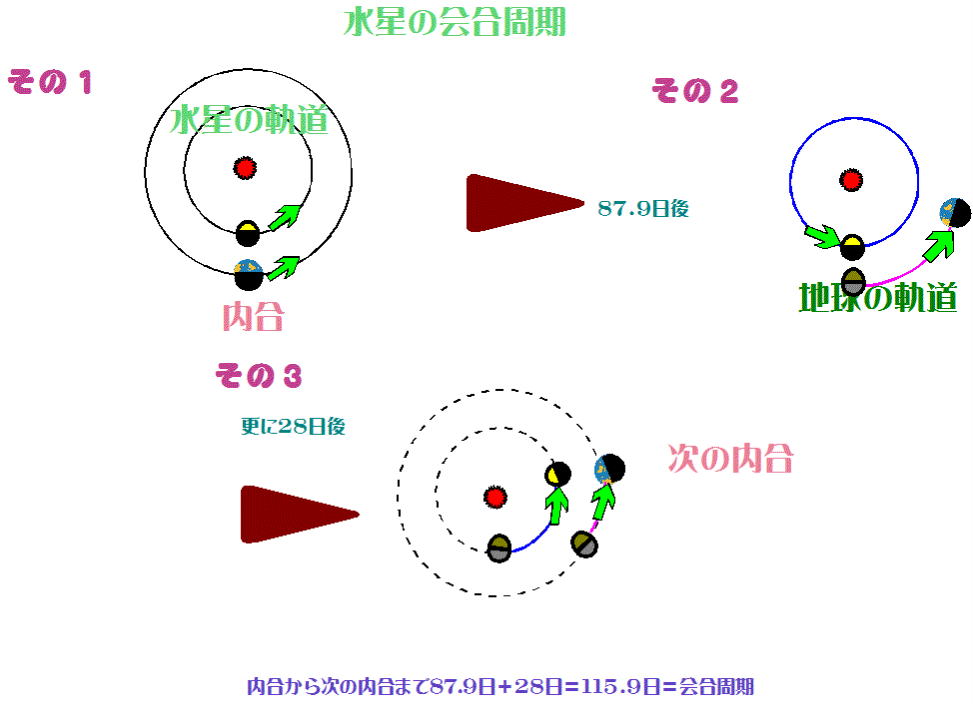
図-7
図-7は水星の会合周期の概念図である。
「その1」ある日、水星が内合である様子を示している。水星は、太陽に最も近い惑星で公転速度は大きい。87.9日後には
「その2」水星は1公転してスタート地点に戻ってきている。一方、地球は365日で360°公転なので87.9日間ではせいぜい86°公転する程度である。
「その3」更に28日経つと水星は地球に追いつき、再び内合となる。
水星の会合周期=内合から次の内合まで=は115.9日となる。

|
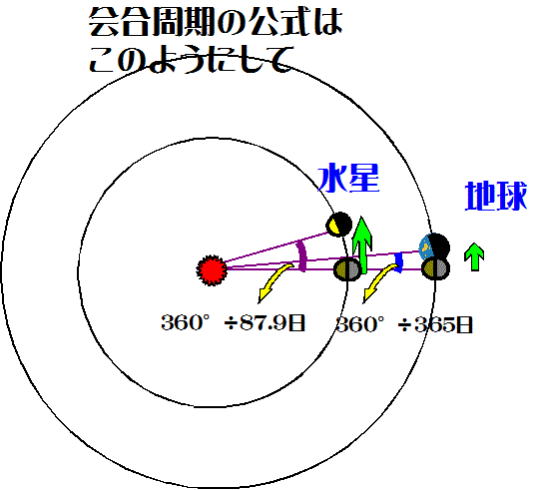
図-8
|
では水星の会合周期115.9日はどのようにして出てきたのだろう。
図-8はある日内合だったのが、1日後の位置を表している。
韋駄天の水星は1日あたり360°÷87.9日進む。一方地球は360°÷365日
進むので、地球は、1日あたり角度にして360°÷87.9日-360°÷365日だけ
水星に置いてきぼりを喰うことになる。これがたまりに溜まり、S日か
かって360°になると次の内合、会合となる。
したがって次の式が成り立つ
。
(360°÷87.9日-360°÷365日)✕S日=360°
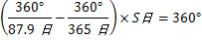 -① -①
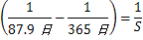 -② -②
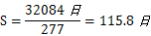 -③ -③
内惑星の会合周期の公式
上の②式がベースになる。
内惑星の公転周期をP(日)(P=planet)、地球の公転周期をE(日)、
会合周期をS(日)とすると
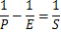
このようにして、内惑星(外惑星も含めて)の会合周期を観測・測定する
ことによって、内惑星の公転周期を求めることができた。
|
次に外惑星の代表、火星の会合周期を見てみると図-9のようになる。
今度は、地球の方が火星より公転速度が大きく、地球が火星より先行する。
水星の会合周期にくらべて気づくことは、「なかなか会合しない」、「会合周
期が長い」ということ。(これについては後述)
図-8に倣い、外惑星の会合周期の公式の導出を行う。考え方は図-8で
地球が内側(太陽側)に来る違いがあるだけで、皆さんそれぞれ考えて見ては
どうだろう。
|
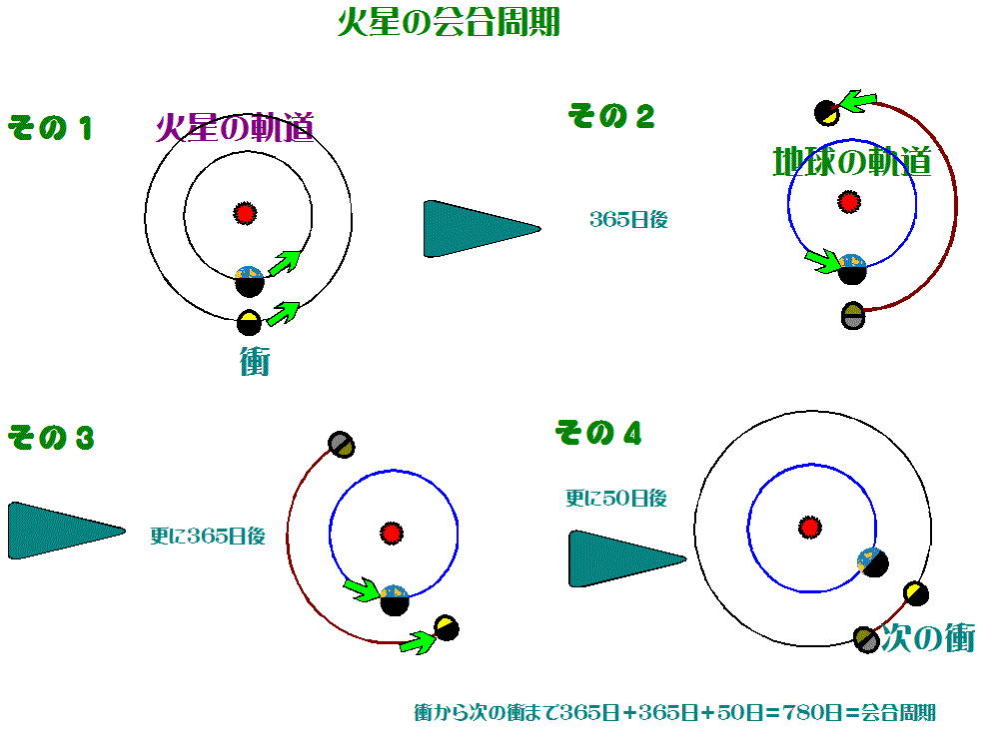
図-9 |
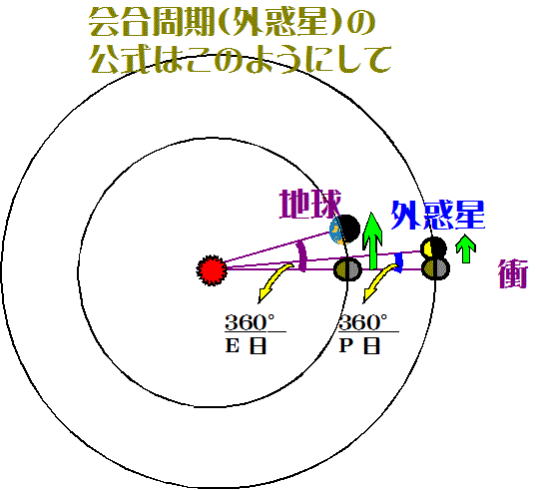
図-10 |
外惑星の会合周期の公式
外惑星の公転周期をP(日)(P=planet)、地球の公転周期をE(日)、会合周期をS(日)とすると 地球は1日あたり 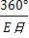 、 、
外惑星は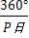 公転するので 公転するので
、角度にして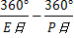 の差がつく。 の差がつく。
S日間で360°の差がつくと次の衝=会合になるので、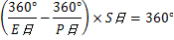
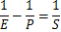 -外惑星の会合周期の公式 -外惑星の会合周期の公式
 |

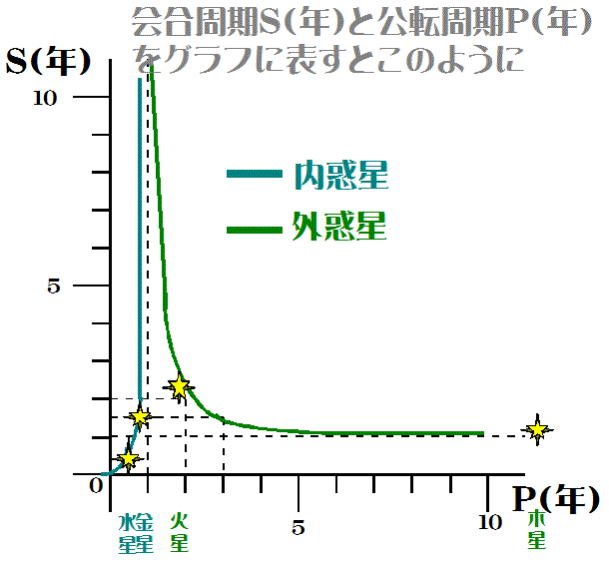
図-11
|
場合に分けてグラフを描く
(1) 内惑星について
内惑星の会合周期の公式から
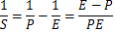
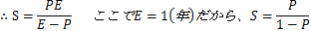
内惑星であるから、P<1、
P=0 → S=0
P=0.24(水星の公転周期)→ S=0.31
P=0.5→ S=1
P=0.61(金星の公転周期)→ S=1.598
P≒1→ S≒∞
この関係をグラフ化すると、青色の曲線で示される。
この関係をグラフ化すると、青色の曲線で示される。
◎内惑星(2つしかないが)0~∞(年)ということ
(2) 外惑星について
外惑星の会合周期の公式から
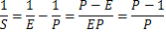 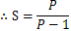
外惑星であるから、P>1
P≒1→ S≒∞
P=1.88(火星の公転周期)→ S=2.14
P=2 → S=2
P=3 → S=1.5
P=11.8(木星の公転周期) → S=1.09
P≒∞ → S≒1
この関係をグラフ化すると、緑色の曲線で示される。
◎外惑星(4つしかないが)1~∞(年)ということ
|

 朔望月 朔望月
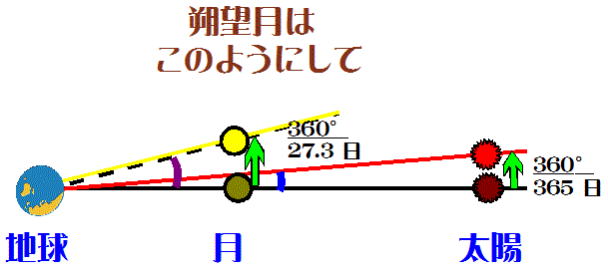
朔望月とは滿月(新月)から滿月(新月)までの日数。月は27.3日で公転し、地球は365日で
太陽を中心
に公転している。
考え方として、太陽が地球を中心に365日で公転しているとして、朔望月は何日か求めよ。
右図はある日新月の状態を示しており、1日後の月、太陽の位置をあらわしている。
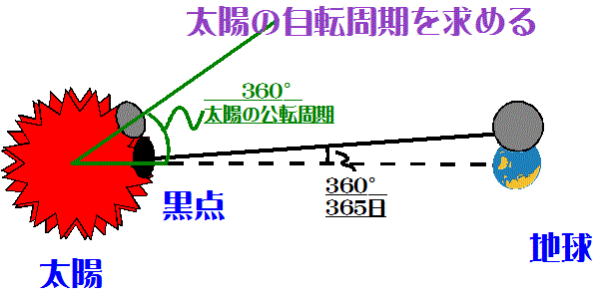
 太陽の自転周期を求める 太陽の自転周期を求める
。
右図はある日新月の状態を示しており、1日後の月、太陽の位置をあらわしている。 太陽にある黒点
(太陽の緯度=日面緯度にして5~40 °に多く発生する)が中央に観測されてから、再び太陽の中央に観
測されるまで28.3日(会合)かかったとする。
太陽の自転周期を求めよ。
【解答】
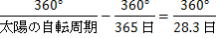
 ・・・答え ・・・答え
|
【解答】
朔望月をSとすると 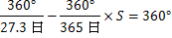
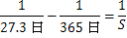
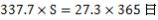
 ・・・答え ・・・答え
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|


