  
|
ケプラーの法則を学ぶ前に、楕円の性質について学んでおこう。
楕円は円とはまた違って「奥行きが深く面白い図形である」と思えたら万歳。
実際に紙(画用紙・ケント紙)と鉛筆・凧糸・画びょうを用意して、楕円を描くの
が楽しい。
描いて「ほう、ナルホド」そう思うこと間違いなし。
ただ、画びょうを机に向かって差し込んでは机に傷がつきお母さんや先生
に叱られます。紙(画用紙・ケント紙)の裏側から表に向かって画びょうを刺し、
びょうの先端に凧糸を緩まないように結ぶと良い。
|
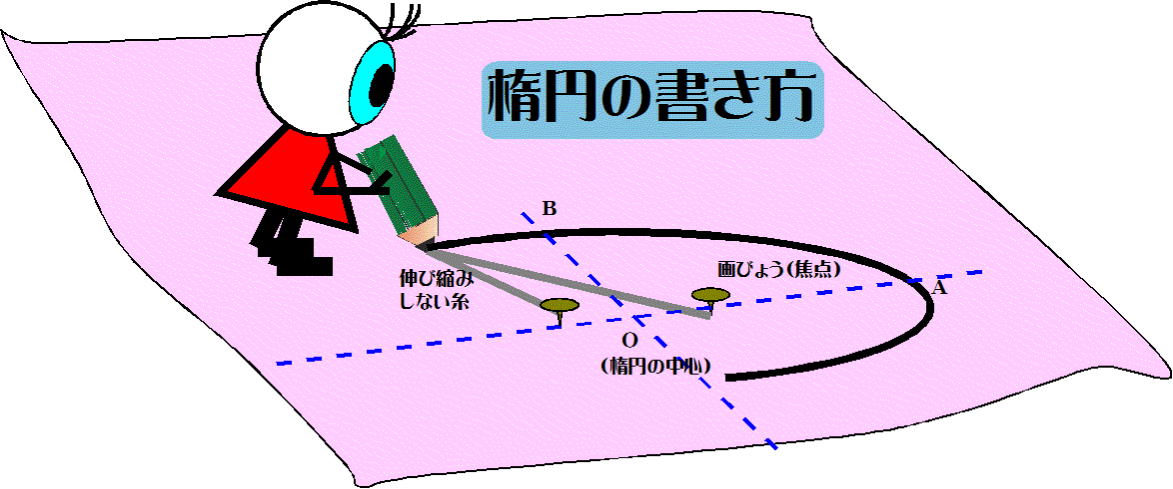
図-1
|
図-1のひとみちゃんのように、凧糸が緩まないように鉛筆を動かしていくと楕円が
描ける。
この時、鉛筆の先を楕円を描く際の「動点P」、2つの画びょうを通る直線を「長軸
方向」、2つの画びょうの中間を通りかつ長軸方向と直角に交わる直線を「単軸方向」、
「長軸方向」と「単軸方向」の直線の交点を「楕円の中心」という。「長軸方向」の直線
と「単軸方向」の直線は描かれた楕円によって切り取られる。図-1では2倍のOAの
長さが「長軸」、2倍のOBの長さが「短軸」になる。 |
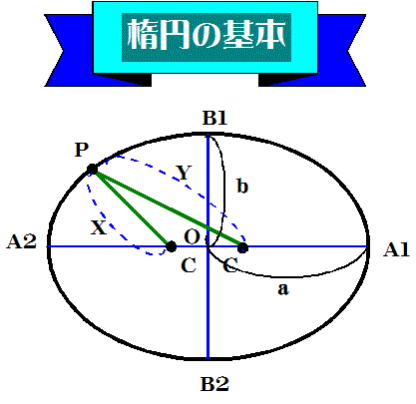
図-2
|
図-1と図-2を良く照らし合わせて見てほしい。
画びょうを押した場所が図-2の楕円の中心OからCだけ長軸方向にずれている。
図-2の緑の折れ線(X+Y)は図-1の凧糸にあたり、鉛筆の先は動点Pにあたる。
凧糸は伸び縮みしなく、楕円を描く時は緊張させて描くのだから、
X+Y=一定・・・①式 となる。
次に動点PがA2の位置に来た時を考えよう。
X=a-c、また Y=a+c
①式より X+Y=a-c+a+c=2a・・・②式
|
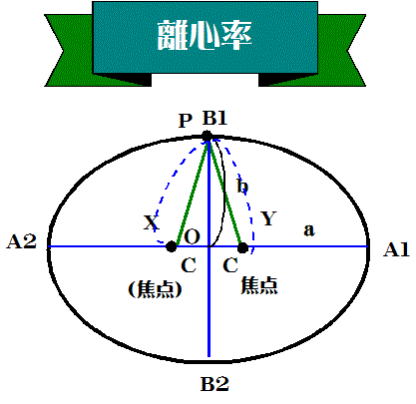
図-3
|
図-1の楕円の描き方で、2つの画びょうの距離を様々にとって描くと楕円の形は
様々になる。
すこし考えれば分かるように、2つの画びょうを近づければ楕円は円に近くなり、重な
れば円になる。
離心率(e)は楕円の中心から焦点(焦点までの距離)がどれほどずれているか、
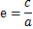 で定義される。c=0でe=0、円となる。 で定義される。c=0でe=0、円となる。
図-3で動点PがB1に来たとすると、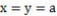
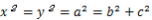
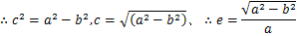
|
 
|
|


|
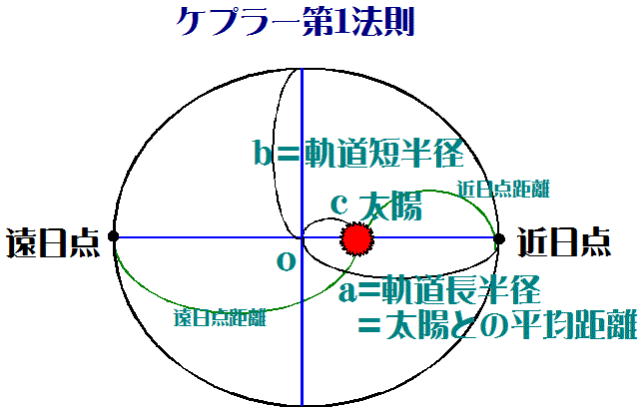
図-4
|
楕円には焦点が二つある(図-3)。そのうちの一方に太陽が位置しているとケプラーは言う。
惑星の軌道の太陽からもっとも離れた一点を遠日(えんじつ)点、最も近い点を近日(きんじつ)点という。
遠日点距離=遠日点~太陽、記号でrL、
近日点距離=近日点~太陽、記号でrSとすると
rL=a+c、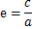 (離心率の項参照) より rL=a+ea=a(1+e) rS=a-c、 rS=a-ea=a(1-e) (離心率の項参照) より rL=a+ea=a(1+e) rS=a-c、 rS=a-ea=a(1-e)
また大事なことは、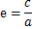 との関連で rL+rS=2a (図-4をじっくり見る)また、 rL-rS=2c との関連で rL+rS=2a (図-4をじっくり見る)また、 rL-rS=2c
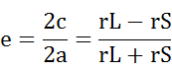 重要な公式 重要な公式

|
  
|
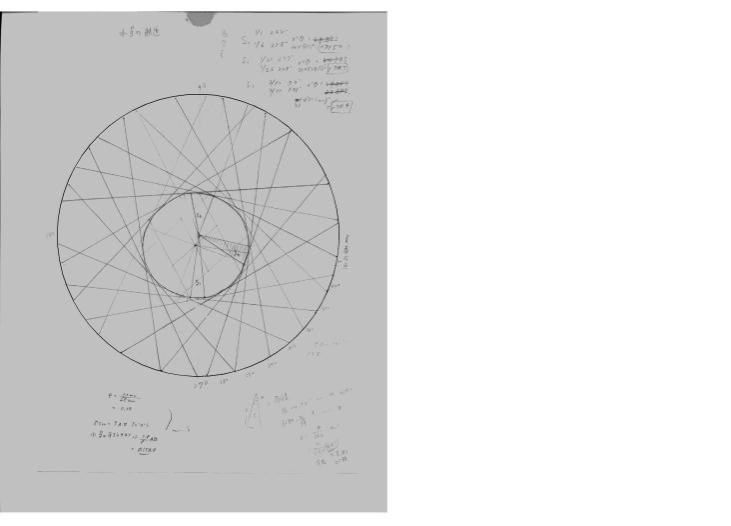
図-5
|
図-5は地球の軌道が円であるとして、最大離角(東方、西方)の位置にある水星を観測し、地球から水星の観測される方向
を直線で現したものである。これだけでは水星は直線上のどこ位置するか決められない。
水星が最大離角であるとき、様々に観測日を変えて水星の観測される方向に直線を引くことによって、水星の
軌道は「外堀を埋められる」ように決められていく。(図-6:図-5の解説図)
|
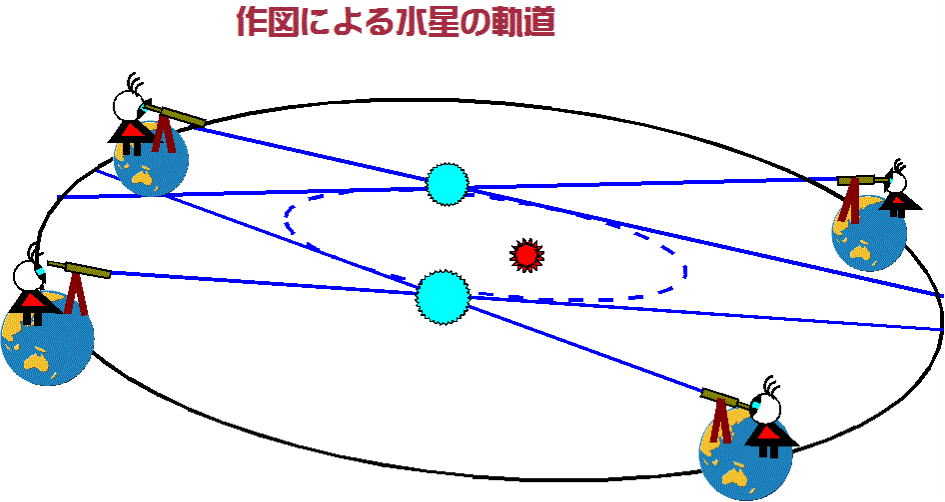
図-6
|
図-5の外側の円(作図では半径8cm)は地球の軌道、多数の直線に囲まれて描かれた小さい楕円が水星の軌道
である。図が不鮮明であるが時計の「1時の方向」が長軸方向で、3つの扇形の中心が集まっているところが太陽
(楕円の焦点)、その下の黒い点が楕円の中心になる。
この作図から得られた水星の離心率eは0.19(理科年表によると0.2056)、平均距離aは0.35AU(同、換算値で0.
387AU)である。結構正確な値が得られていると思いませんか。
図-5、水星の軌道内に三つの扇形が描かれている。これは次のケプラーの第二法則を検証しようとして作図したもの。

|


|

図-7
|
ケプラーの第二法則=「面積速度一定の法則」?
「なに、それ。」「図-6の扇形saa'と扇形sbb'の面積が等しい-って言われても、図は悪くてそうは見えない!」そう言われるでしょう。
では。
|
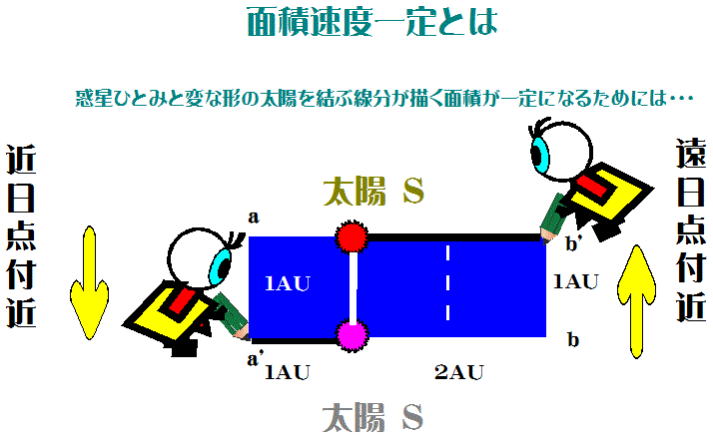
図-8
|
むかしむかし、惑星「ひとみ」があった。近日点付近、遠日点付近でそれぞれ1か月公転(直線的に)し、その速度が1AU/1か月だったと
する(図-7)。(1AU=1 astronomical unit=1天文単位=地球~太陽間の平均距離=1.5✕108km)
そうすると、面積速度は近日点付近では1AU2/1か月。(1AU2 = 青の正方形の面積)
同じように、遠日点付近では2AU2/1か月。(2AU2 = 青の長方形の面積)
これでは同じ1か月という時間で惑星「ひとみ」と太陽が結ぶ線分の描く面積が1:2で等しくならない。
ではどうしたら等しくなるか?近日点付近での速度を1AU/1か月で一定にするなら、遠日点付近での速度を半分にすればよろしい-
「近日点より2倍離れた遠日点では、1か月でbb'間は0.5AUしか進まない。速度が半分になる」これが面積速度一定の意味である。
簡単に言えば「太陽に近くなると速く、太陽から遠くなると遅く公転する」-ということ。
|
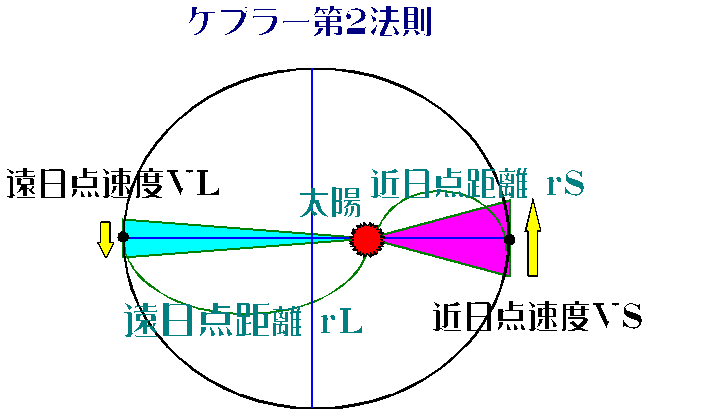
図-9
|
センター試験受験関わるのは図-9にまつわる問題である。
ケプラーは「惑星と太陽を結ぶ線分が一定の時間に描く面積は一定である」ことを見いだした。図-9に示されるように
青色と桃色の扇形の面積は同じである-という。
ここで青色と桃色の扇形をそれぞれ青色と桃色の「三角形」に近似し、その面積について考える。
青色の三角形の面積= 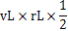
桃色の三角形の面積= 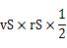
「惑星と太陽を結ぶ線分が一定の時間に描く面積は一定である」から
青色の三角形の面積=桃色の三角形の面積
 、 、 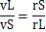 ・・・公式 ・・・公式
つまり


水星の軌道長半径(a)を0.39AU、平均公転速度を48km/s、近日点距離を0.31AUとする。近日点速度、遠日点速度それぞれを求めよ。
|
【解答】
まず問題文に示されたデータを図に書き表すこと。図を書くことによって解答への道筋が見えてくる。
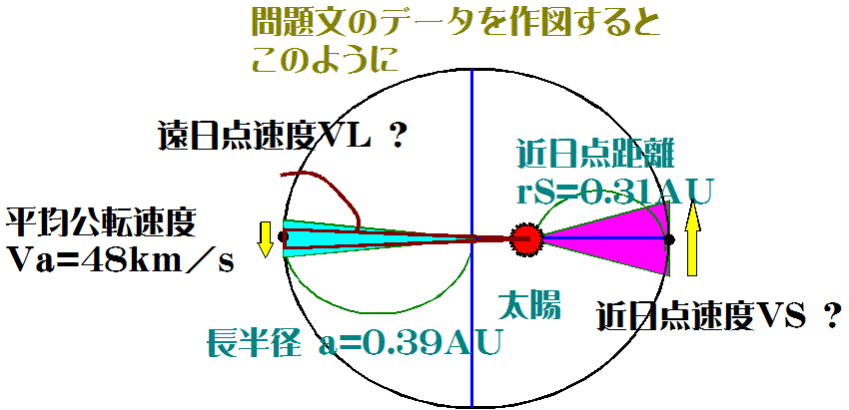
① 近日点速度を求める
ケプラーの第二法則  より より 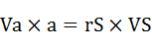
48km/s✕0.39AU=0.31AU✕VS VS=60.49km/s-答え
② 遠日点速度を求める
rL=a+a-rS=(長半径+長半径-近日点距離)=0.39+0.39-0.31=0.47AU
48km/s✕0.39AU=vL✕0.47AU VL=39.83km/s-答え

ケプラーの第二法則 は、「太陽に近ければ速く、遠ければゆっくりと公転している」ということをいっている。 は、「太陽に近ければ速く、遠ければゆっくりと公転している」ということをいっている。
どうしてこのような関係になるかというと、「週末課題 No.2」やHP「25 海洋 ⑩潮汐」で扱われた「太陽の引力」が惑星の位置によって異
なるから。
そして一方では、円運動を行うと物体は外側に押しやられる力=「遠心力」を受けることである。日常、遠心力を受けるような経験は、バス・
電車に乗っている時など良くあることと思う。
|
図-10
|
銀河電鉄の電車は左回り(反時計回り)のカーブを通過中。電車
内のつり革も、乗客も外側に向かう遠心力を受けている。
車体も同じ外側へ向かう遠心力をうけるので、電車は外側に飛び出
て脱線する恐れがある。
それを防ぐために、カーブ付近のレールには高低差を付けてある。外
側のレールは内側より少し高くし、通過する車体を内向きに傾斜させるこ
とによって車輌に加わる重力の分力を内側に向かわせる。そして遠心力
に釣り合わせ、電車が外に飛び出さないような設計になっている。
遠心力の大きさは、通過する電車(円運動を行う物体)の速度の二乗
に比例するので、設計されたスピード以上で走れば釣り合いを越えてし
まい、電車はレールに「乗って」カーブを曲がりきれなくなる。
ある程度スピードを出して走ることのできる道路のカーブもよく見ると、
電車のレールと同じように、高低差(カント)がつけられている。制限速度
を守って走らなければならないのは言うまでもないことで、「運転技術に
長けているから」とスピードを出すのは事故の元。
|
では物体(惑星)が円(楕円)運動をし続けると、物体(惑星)は遠心力を受け続け、あたかも「渦巻き」のように末広がりな軌跡を描くのか?
というとそうはならなく、太陽の引力と遠心力が釣り合い、物体(惑星)は一定の軌道を描く。
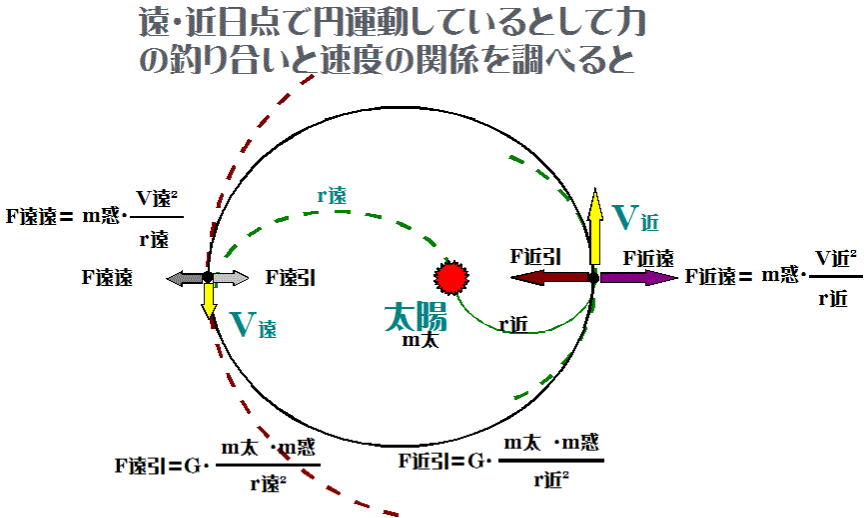
図-11
太陽の質量をm太、惑星の質量をm惑、遠日点距離をr遠、近日点距離をr近、万有引力定数をG、遠日点速度をV遠、
近日点速度をV近、遠日点における惑星への引力をF遠引、遠日点における惑星に働く遠心力をF遠遠、近日点における
惑星への引力をF近引、近日点における惑星に働く遠心力をF近遠とすると、
遠日点における惑星に働く力は、遠心力と太陽の引力で、 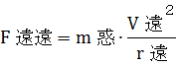 、 、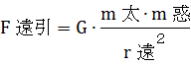
遠心力と太陽の引力が釣り合っているので、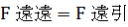 、 、 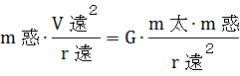
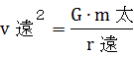 、 、 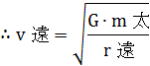
同様に近日点において、 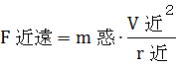 、 、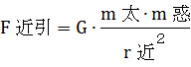
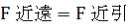 、 、 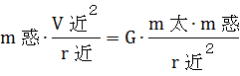 、 、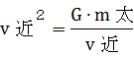 、 、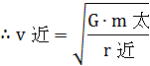
v遠は、G・m太(一定の値)をr遠(r遠>r近)で割った平方根。故にv遠<v近になる。
簡単に言えば、「近日点では太陽に近く引力が大きいため、公転速度を速くして遠心力を大きくしなければならない惑星の
事情がある」と思えばいい。
|


|
ケプラーはティコ・ブラーエ(デンマーク)の下で火星の逆行につい
て研究を行ていた。
ティコは54歳で病死し(1601年)、膨大な観測データが弟子のケプラー
にもたらされた。
ケプラーは観測データを下に1609年第一・第二法則、1619年第三法則
を発表した。
というわけで、以下に惑星の公転周期・平均距離他のデータを示すと。
|
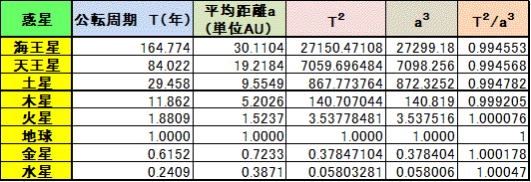
表-1
|
ケプラーは、「Tの2乗は、aの3乗に比例する」と言っているのだから、比例定数を仮にk とすると、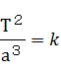 上の表の右端の値を見てほしい。 上の表の右端の値を見てほしい。
k の値は1/100の誤差の範囲で「1」におさまっている。
美しいバランス・規則に則って惑星が運行している。まさに「調和の法則」といえる。ビバルディではないが、「調和の霊感」とまで言えるので
はないだろうか。
それでは、上のデータをグラフ化するとどうなるかというと。
|
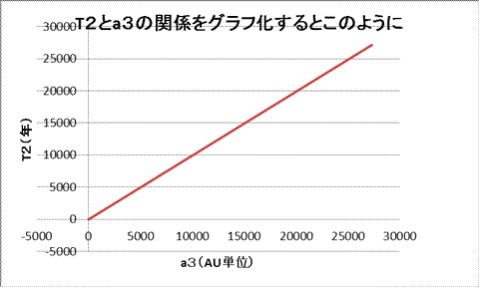
図-12
|
「惑星の公転周期Tの2乗は、惑星の太陽からの平均
距離a(半長軸)の3乗に比例する」と言われると、なんだか七面倒
くさく思ってしまうが、y=a・x のグラフと同一、yはxと比例関係にあ
るということと同じにすぎない。
しかし地学を学ぶ皆さんには、「値が0.005から27000まで渡る
のに、 こんな小さなグラフに表したら、直線になるのは当たり前
じゃないの」 という人もいるかもしれない。
と言うわけでもう少し詳しいグラフを示して説明したい。
(図-13,14)
|
「両対数方眼紙」というのがあって、これは図示しようとする値が幅広くても表示できるメリットがある。縦横等間隔に1メモリ進むと、値が一桁
大きくなる。(原図はB5版)
この両対数方眼紙に、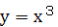 、 、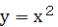 、 、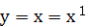 、 、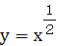 、 、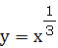 の5つのグラフを描くと どうなるか、それを示し の5つのグラフを描くと どうなるか、それを示し
たのが図-13である。
|
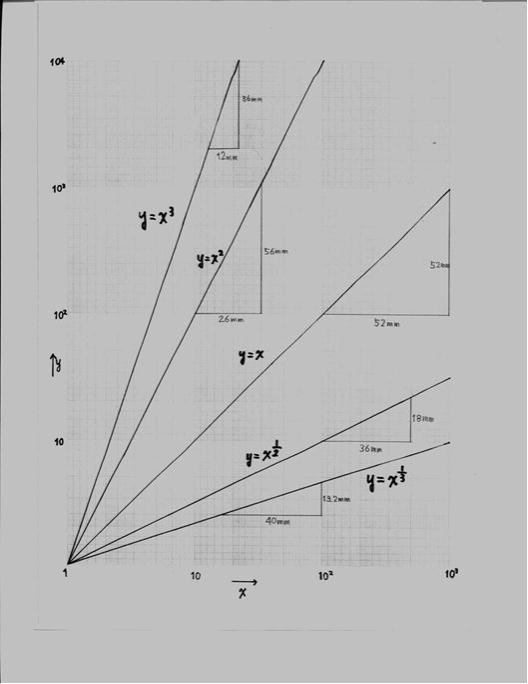
図-13
|
この時、両対数方眼紙に描かれたそれぞれのグラフの「傾き」は、関数の「Xの指数」とが一致していることが分かる。
例えば、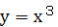 の傾きをしらべると、X方向に12mm、Y方向には36mmで、傾きは36mm÷12mm=3でXの指数部分 の傾きをしらべると、X方向に12mm、Y方向には36mmで、傾きは36mm÷12mm=3でXの指数部分
の3に一致する。
以下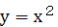 では26mm分の52mm(グラフで56mmとあるのは52mmの誤りです)、 では26mm分の52mm(グラフで56mmとあるのは52mmの誤りです)、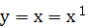 では52mm分の52mm、 では52mm分の52mm、
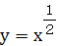 では36mm分の18mm、 では36mm分の18mm、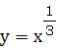 では40mm分の13.2mmとなり、グラフの傾きはXの指数部分に一致することがわかる。 では40mm分の13.2mmとなり、グラフの傾きはXの指数部分に一致することがわかる。
以上のことを予習した上で、下の惑星のデータを両対数方眼紙にプロットしてみると、それは図-14になる。
|
|
惑星
|
公転周期 T(年)
|
平均距離a (単位AU)
|
|
海王星
|
164.774
|
30.1104
|
|
天王星
|
84.022
|
19.2184
|
|
土星
|
29.458
|
9.5549
|
|
木星
|
11.862
|
5.2026
|
|
火星
|
1.8809
|
1.5237
|
|
地球
|
1.0000
|
1.0000
|
|
金星
|
0.6152
|
0.7233
|
|
水星
|
0.2409
|
0.3871
|
|
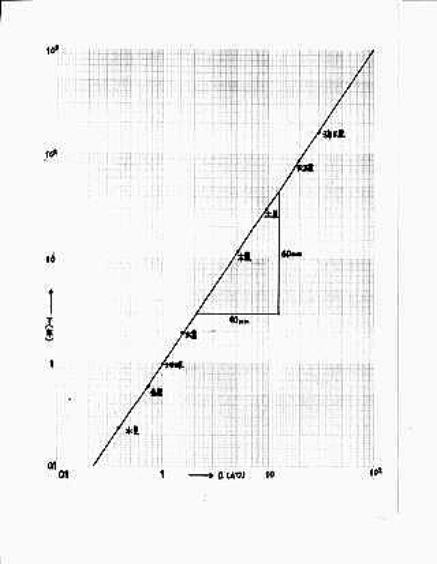
図-14
|
図-14のグラフの直線の傾きは60mm/40mm=3/2で、図-13での予習したことに併せて考えると、公転周期
T(年)と惑星の平均距離a(AU)の関係は 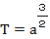 となる。 となる。
両辺を2乗、 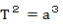 となり、ケプラーの第三法則である。 となり、ケプラーの第三法則である。
|
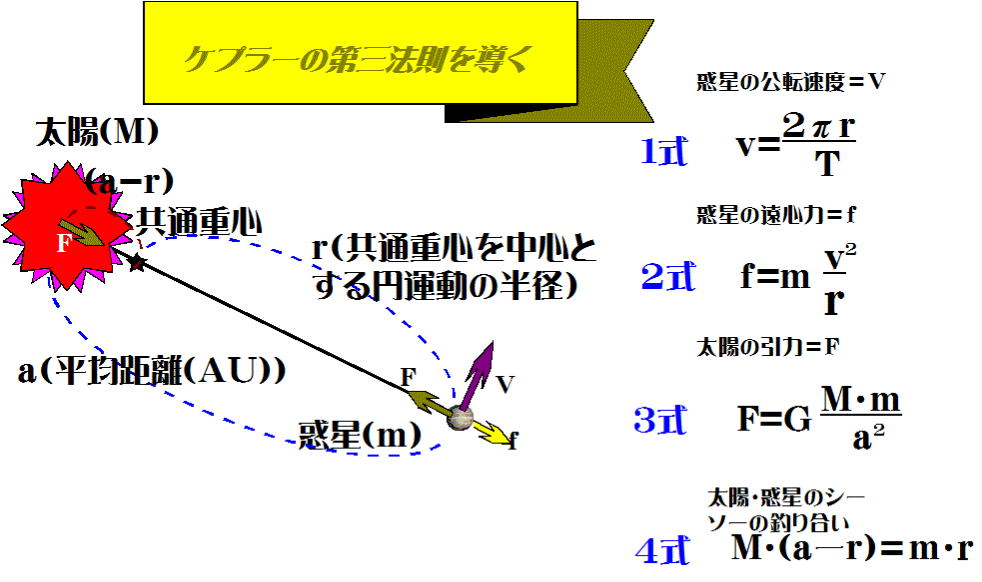
図-15 |
ケプラー第三法則の導出
惑星は太陽の引力(3式)とこれに釣り合う遠心力(2式)をうけて、等速円運動、速さv(1式)で公転する。図では共通重心の位置は太陽から
十分離れた位置にあるが、実際はほとんど太陽の中心にある。
さて惑星は太陽に引き寄せられることもなく、また太陽から離れ去ることもないから、力の関係は
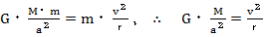 -5式とする。 -5式とする。
5式において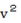 は1式より、 は1式より、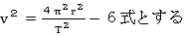
4式より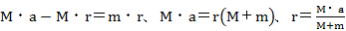 これを7式、この値を これを7式、この値を
6式と7式を5式のv2、r に代入して
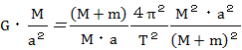 、 、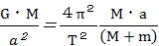

Mは太陽の質量。mは惑星の質量(太陽質量)。惑星最大の木星でも10-3
太陽質量で極めて小さくmは無視できる。したがって
 となり となり 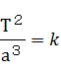 で一定の値をとる。 で一定の値をとる。
ここでケプラーの第三法則を地球に適用すると、T=1(年)、a=1(AU)であるので、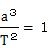 k=1という何とも「ファンタスティック」 k=1という何とも「ファンタスティック」
な定数になってしまうのである。
更に付け加えることがあるとすれば
逆にケプラーの第三法則は、Tが決まればaが自動的に決まることを意味しており、惑星は太陽から好きな距離を離れて、好きな公転周期で
公転できないということであり、更には地球を周回する人工衛星にもこの法則が当てはまる-ということである。
|

【演習問題 1】 
Tuttle彗星の公転周期Tは13年、近日点距離は1AUである。以下の問いに答えよ。
(1)平均距離を求めよ。
(2)遠日点距離を求めよ。
(3)離心率を求めよ。
(4)近日点速度は遠日点速度の何倍か。
ただし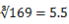 として計算せよ。 として計算せよ。
(データは理科年表を参照、改変しています)
【解説・解答】
まず与えられたデータをもとに作図し、どのような公式を用いれば答えに至るかを考える。
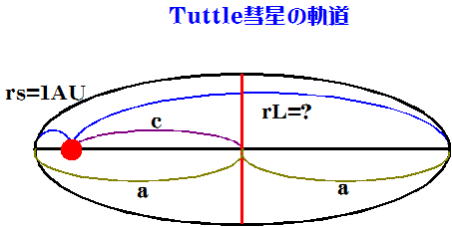
(1) まず、公転周期Tが13年と分かっている。必ず地球を引き合いに出す。
ケプラーの第三法則より、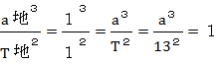
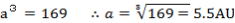 -(1)平均距離 答え -(1)平均距離 答え
(2) 次にrS+rL=2a ∴1AU+rL=11AU、rL=10AU-遠日点距離 答え
(3) 離心率 eは 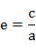 で求められた。c=a-rS=5.5AU-1AU=4.5AU、離心率0.82 答え で求められた。c=a-rS=5.5AU-1AU=4.5AU、離心率0.82 答え
(4) ケプラー第二法則より 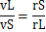 、 、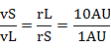 、10倍-答え 、10倍-答え
【演習問題 2】 
公転周期T=2√2年の惑星があり、円軌道を描いて公転しているものとする。以下の問いに答えよ。(有効数字2桁)
(1)平均距離を求めよ。
(2)この惑星は内惑星となるか、外惑星となるか。
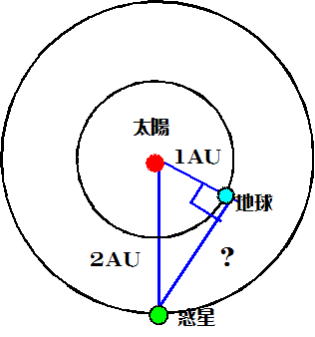
(3)地球をこの惑星から観測したとして、地球が最大離角となった時の地球~惑星間の距離はいくらか。
(4)会合周期を求めよ。
【解説・解答】
(1) ケプラー第三法則より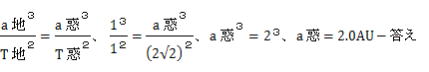
(2) 1AU(地球の平均距離)より大きいから、外惑星-答え
(3) 図より、1-2-√3の直角三角形であることが分かる。したがって外惑星~地球間の距離は√3=1.73、1.7AU-答え
(4) 会合周期の公式、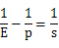 より より 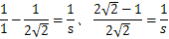 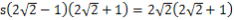
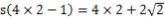 、 、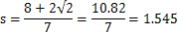 1.5年-答え 1.5年-答え
【演習問題 3】 
Schaumasse彗星の近日点距離は1.2AU、遠日点距離は6.8AUである。以下の問いの答えよ。(有効数字2桁)
(1)遠日点速度は近日点速度の何倍か。
(2)離心率はいくらか。
(3)平均距離距離を求めよ。
(4)公転周期を求めよ。
(データは理科年表を参照、改変しています)
【解説・解答】
(1) ケプラー第二法則 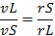 より より 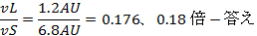
(2) 離心率を求める公式 
(3) 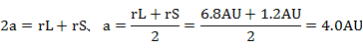 -答え -答え
(4) ケプラーの第三法則より 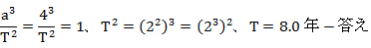
【演習問題 4】  祝 初優勝 稀勢の里関 祝 初優勝 稀勢の里関
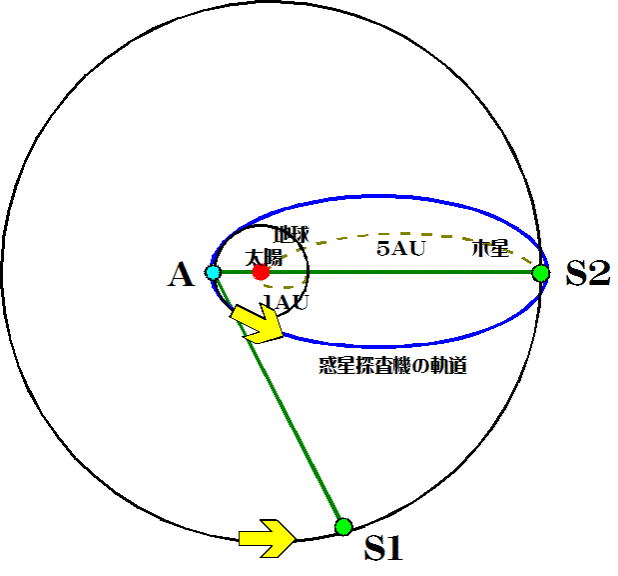
地球から木星へ惑星探査機を打ち上げ、観測に向かわせようとしている。惑星探査機は太陽を焦点とする楕円軌道を描き、
木星に接近する。地球、木星はともに円軌道を描いて公転しており、地球、惑星探査機、木星は同一平面上を公転する。図は天の
北極側から見て、各天体は矢印の方向に運動している。
惑星探査機は地球・木星の引力に影響されることなく公転するものとして、以下の問いに答えよ。(有効数字2桁)
(1)木星の公転周期は何年か。
次のうちもっとも適当なものを選べ。
① 0.25年 ②0.61年 ③1.88年 ④11.9年 ⑤29.5年
(2)惑星探査機の平均距離はいくらか。
(3)惑星探査機の近日点速度は遠日点速度の何倍か。
(4)惑星探査機の公転周期は何年か。
次のうちもっとも適当なものを選べ。
① 0.52年 ②1.62年 ③3.68年 ④5.19年 ⑤14.5年
(5)惑星探査機がAを出発し、S2で木星に出会うためには木星の位置S1を確定しなければならない。∠S2・A・S1はおよそ何度
となるか。次のうちもっとも適当なものを選べ。
① 60° ② 64° ③ 78° ④ 84° ⑤ 87°
【解説・解答】
(1) ケプラー第三法則より、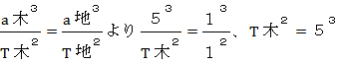
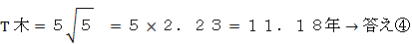
(2) rS探=1AU、rL探=5AU、2a= rS探+rL探=6AU、a=3.0AU-答え
(3) ケプラー第二法則より、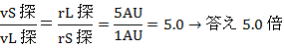
(4) ケプラー第三法則より、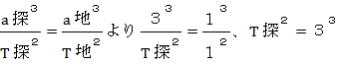
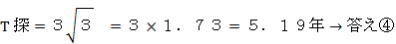
(5) 探査機はA→S2まで 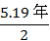 、2.59年要する。一方、木星は360°を11.2年で公転するから、S2から 、2.59年要する。一方、木星は360°を11.2年で公転するから、S2から
2.59年分遡った位置に木星があればよいことになる。したがって、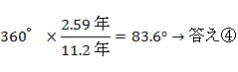
【演習問題 5】  祝 横綱昇進 稀勢の里関 祝 横綱昇進 稀勢の里関
横綱昇進試験問題レベル
赤道上空付近の上空を地球の自転と同じ周期(T=1日)で公転する人工衛星は、地球から観測すると(見えた
とすると)留まったように見えるので「静止衛星」と呼ばれる。
この静止衛星の地表からの高さ(h)をケプラーの第三法則を用いて求める。ただし、月は3.8✕105km(地球の中心
より)を27日で公転しているものとする。また、地球の半径を6.4✕103kmとし、有効数字2桁で求めよ。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|


