 |
中国 黄龍 標高3100mでバス駐車場から標高差450mほど約２時間半ほど登ってたどり着きます。美しい石灰棚 世界自然遺産 |
||
|---|---|---|---|
 |
沖縄・八重山諸島 リスザル。小児麻痺ワクチンの開発に際して、開発されたワクチンの検定などに用いられたということです。 |
１２３ | １２３ |
 |
岩手山（2038m） 岩木山，鳥海山とともに東北の三名山の一座。源太ヶ岳登り途中－秋。 |
１２３ | １２３ |
 |
八ヶ岳 赤岳を望む。山体は輝石安山岩，集塊岩から構成されています。朝日が当たり山の影が山体に映っています－9月 |
１２３ | １２３ |
 |
ナイル川・アレキサンドリア・シエネ（アスワン）の位置関係 （お断り：この地図は Fraid Atiya Press 1:2 000 000 を使用、加工をしています。） |
エラトステネス（Eratosthenes(BC275年～BC194年)）の方法
Eratosthenes
西條敏美(2011)地球から宇宙へ、
恒星社厚生閣より引用
地学では，初めて地球の大きさを測定したのは，エラトステネス(Eratosthenes)であることを学びます。
ところが，難しいことではないのですが，地学を学び始めて，早速つまづく人が出てきます。「地学はわからない」。
「部分を知って、全体を知る」
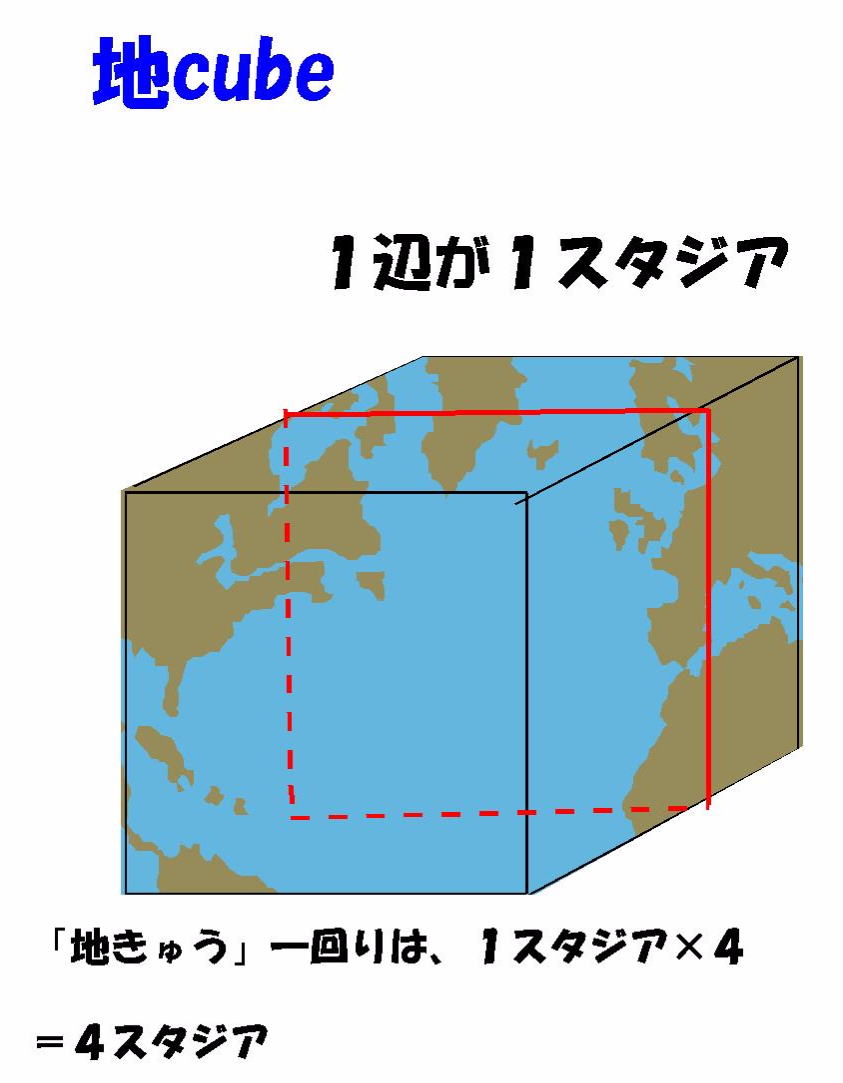
地球が,すでに「球」となっているからやりづらい。そこで、考え方として、角砂糖ような立方体(cube)、
これを「地cube」、無理して「地きゅう」を持ってこよう（下の図参照）。1辺の長さが１スタジア（長さの単位）だったら、この「地きゅう」の一回りの長さ（図の赤い線の長さ）は、４スタジア。一瞬にして分かってしまいます。
一部分の長さを知ることによって、全体の長さ（地球の大きさ）をエラトステネスは求めました。本物の「球」でも、「円」でも考え方は同じ、「部分を知って、全体に膨らませて考える」ことに違いはありません。
地球の全周を求める原理は「扇形の弧の長さは，中心角に比例する」－という関係を用いています。
半径rの円で考えましょう。
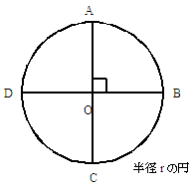
① 半径rの円では
円（中心角360°の扇形）の弧の長さ＝2πr → 円（扇形）の中心角＝360°
② 中心角90°の扇形AOBでは
扇形の弧ABの長さ＝X（分からないものとして）→扇形の中心角＝90°
「扇形の弧の長さは，中心角に比例する」関係から
扇形の弧の長さ：中心角＝別の扇形の弧長さ：中心角 が成り立ちますから，
①，②を比の式に書き表すと，
2πr：360°＝X：90°
X＝2πr・90°/ 360° ＝1/2・πr
この関係から逆に，子午線（子＝北，午＝南，北極，南極をとおる大円）上の２地点間
の距離と扇形の中心角（２地点間の緯度，緯度差）が分かれば，地球の全周を求める
ことができることになります。
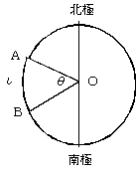
① 扇形AOBでは
弧の長さ＝ι 扇形の中心角＝θ
② 地球では
地球の全周（中心角360°の扇形の弧の長さ）＝X 中心角＝360°
扇形の弧の長さ：中心角＝別の扇形の弧長さ：中心角 が成り立ちますから，
①，②を比の式に書き表すと，
ℓ：θ＝X：360°
X＝ℓ・360°/θ
地球の全周を求めることができます。
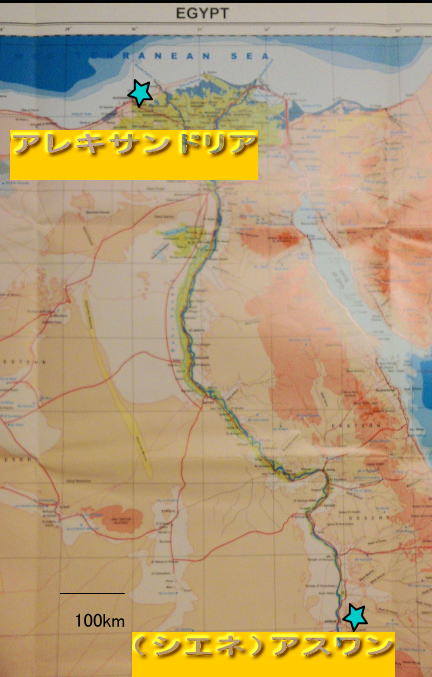
エラトステネスはラクダによる旅行日数から，シエネ（アスワン）とアレキサンドリアの
距離（ℓ）を5000ｽﾀｼﾞｱ，扇形 シエネ（アスワン）－地球の中心－アレキサンドリアの
中心角（θ）を7.2°，地球の全周をXとして
X＝5000ｽﾀｼﾞｱ・360°/7.2°＝250000ｽﾀｼﾞｱ と求めました。
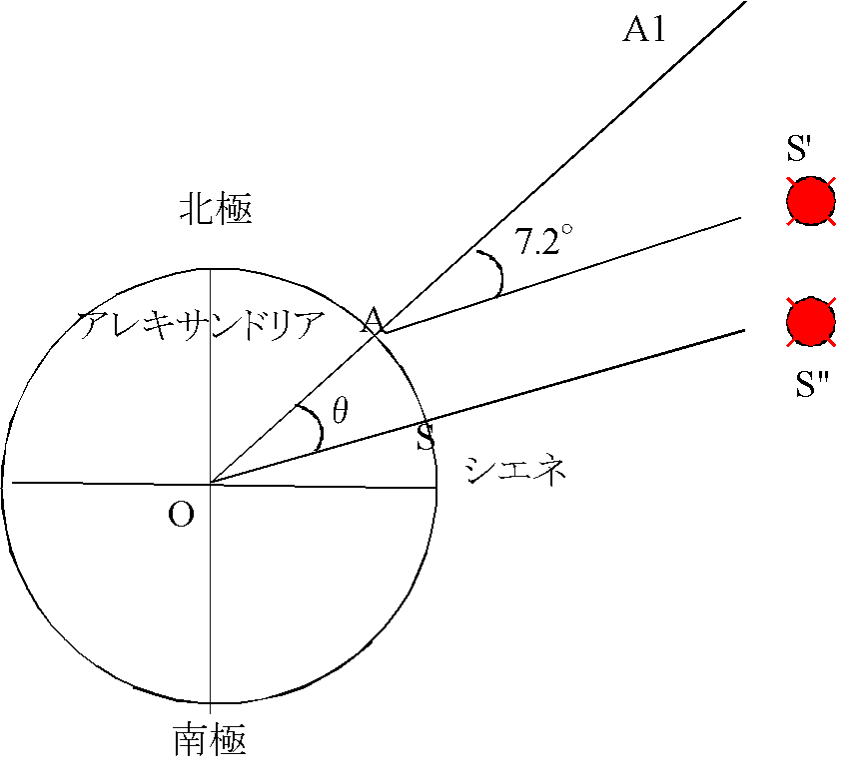
OAを延長した直線OA1は，アレキサンドリアでの天頂方向
OSを延長した直線OS"は，シエネでの天頂方向
毎年 夏至の日の正午 シエネでは太陽が天頂方向に一致（掘り井戸の底を光線が照らした）
一方，5000ｽﾀｼﾞｱ北に離れたアレキサンドリアでは，同じ日の同じ時刻，太陽は天頂
方向から7.2°だけ南に傾いて観測された。太陽は十分に遠くにあるので 太陽光線
S'A//S"Oとして良い。
平行な２直線 S'A，S"Oを直線A1Oが切っています。従って，∠A1 A S'＝∠A O S" θ＝7.2°
冒頭の写真集にアレキサンドリア、シエネ（アスワン）の位置関係をしめす写真を載せてあります。
アスワンと言えば「ダム」。アスワンハイダムは故ナセル大統領の時代、ナイル川（流域6673km）の氾濫をコントロールするために建設された。アスワンの上流280kmには「アブ・シンベル神殿」（巨大岩窟の寺院）があり、ダム建設により水没の危機にさらされた。が、ユネスコが主体となり、「アブ・シンベル神殿」全体を移転（上方へ60m、ナイル川から横へ210m）・保存させている。アブ・シンベル神殿を見たとき、文化遺産を守ろうとする人間の思いの深さに感動しました。）
B.C.6C頃 ターレス
大地の形を平面と考えた。
B.C.500年頃 ピタゴラス
「大地は球形である。球は完全無欠な図形である。」
B.C.400年頃 アリストテレス(B.C.384～322年)月の影が丸い→地球は丸い。
北極星の高度が，北から南へ旅行するとその高度が低くなる。
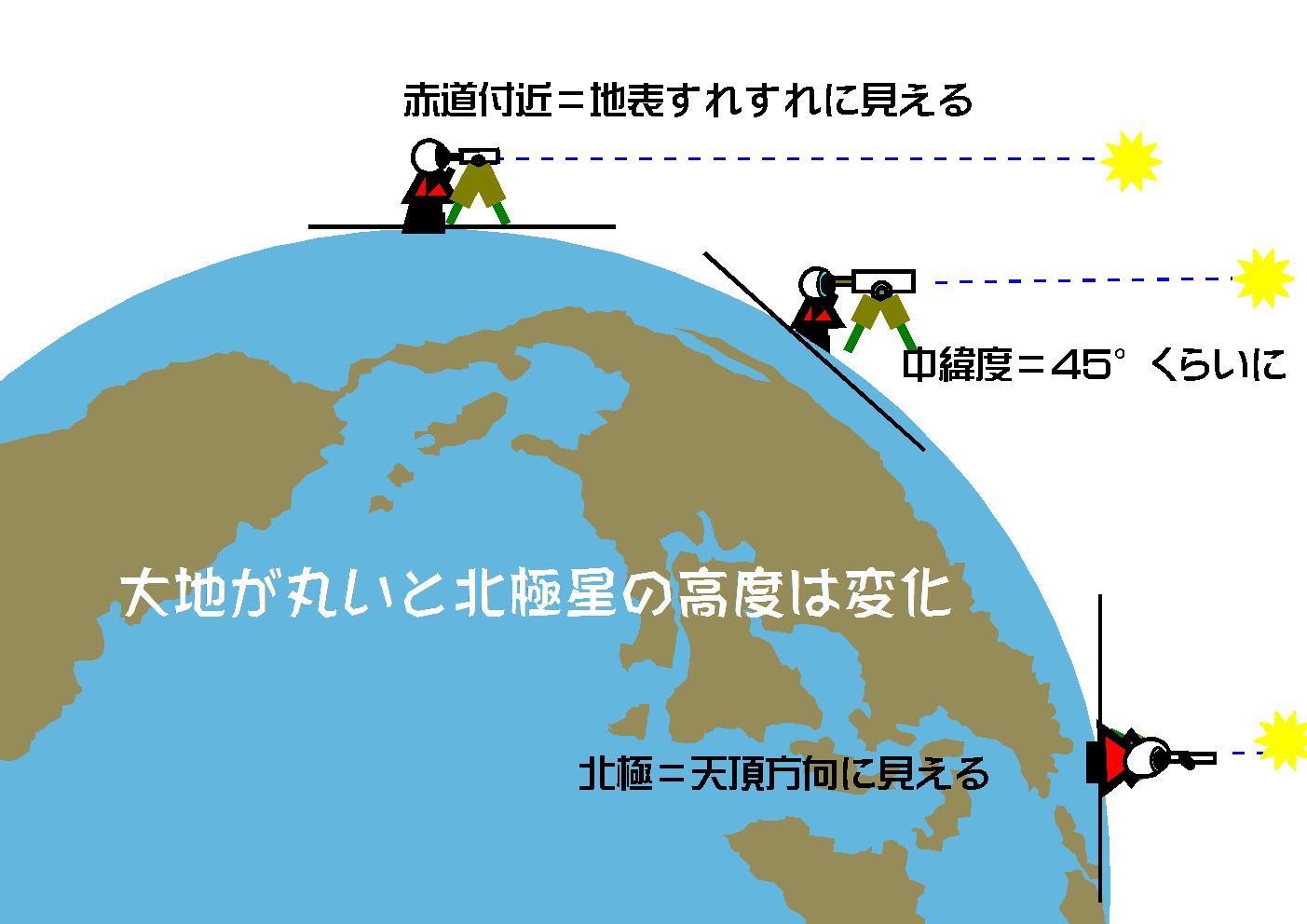
大地が平なら，どこへ行っても北極星の高度は不変のはず。
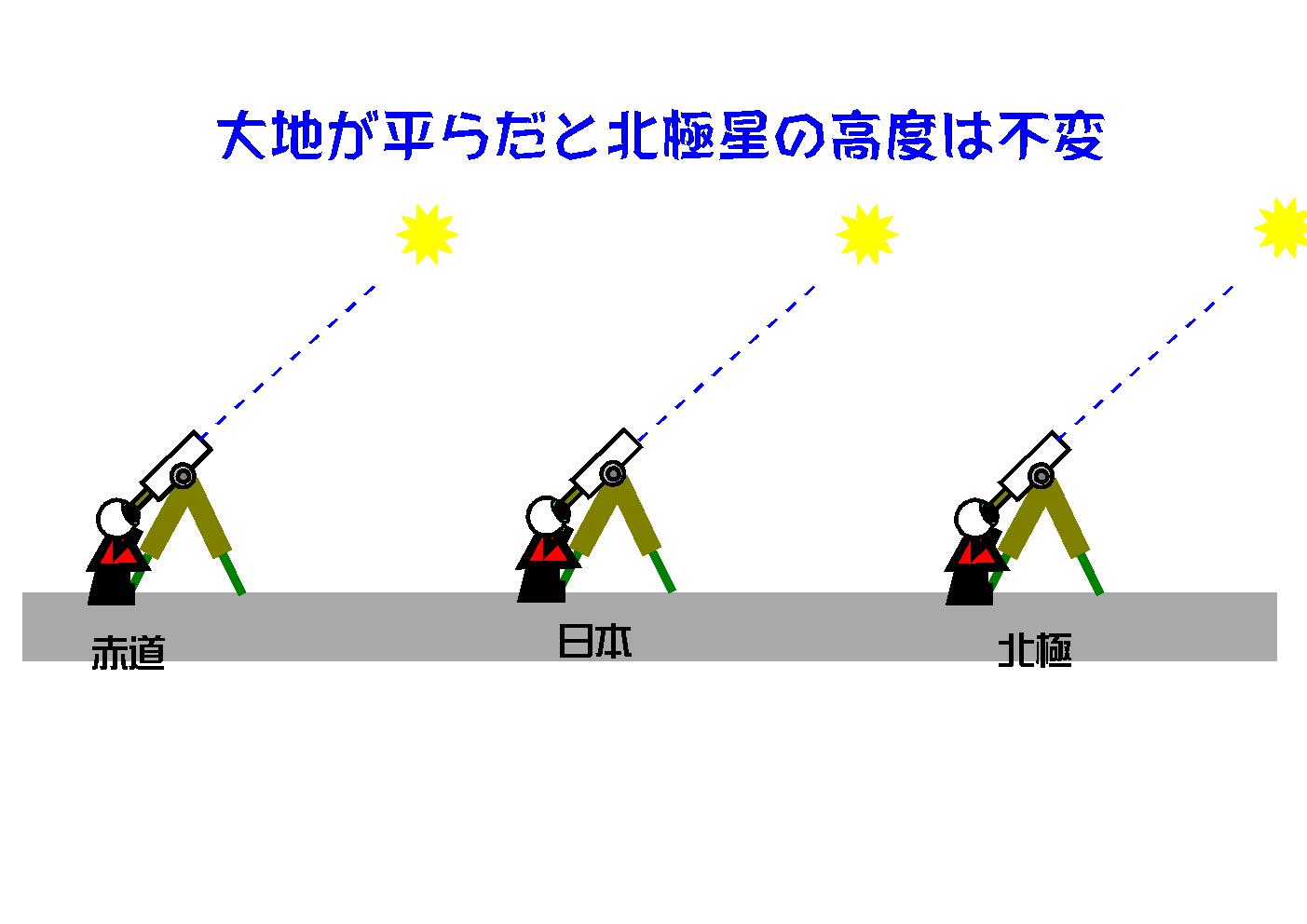
① 古代インド人の考え
大地が亀や象によって支えられていると考えられていた。その時代、亀や象は飛び抜けて優れた存在と思われていた。
② 古代バビロニア人の考え
大地を海がドーナッツ状に取り囲んでいる。さらに海の周りは山脈が取り囲んでいる。山脈は空や星がある天空を支え、山脈を越え た部分は(外側)は特に考えなかった。
③ 古代エジプト人の考え
天空は女神「ヌート」の身体で星々は身体から垂れ下がる飾り－とされた。
④ ターレスの考え(BC6C頃)
宇宙全体は「水」からなる
⑤ アナクシマンドロスの考え(BC6C頃)
地球が宇宙の中心であり、円柱形でその外側は火で満たされている。様々な間隙がありそこから見えるあかりが太陽であり月である。
⑥ フィアオロスの考え(BC6C頃)
地球や太陽を含む全ての天体が、目に見えない宇宙の中心の火の周りを回転している－と考えた。
⑦ アリストテレスの考え(BC4C頃)
大地は球体でその周りを太陽、月、惑星、恒星が回っている天動説を主張した。
⑧ プトレマイオス(AD2C頃)
天動説をもとに天体の動きを数学的に説明した。
⑨ コペルニクス(AD16C頃)
太陽を中心としてその周りを惑星が回る地動説を主張。
コペルニクス肖像
（葛飾区 「郷土と天文の博物館」）
おことわり：写真と説明文は「葛飾区 郷土と天文の博物館」の展示及び説明文によりますが、一部編集しています。
さて地球が丸いことになったところで、
「身長1mのひとみちゃんは何m先まで見ることが出来る」でしょう？
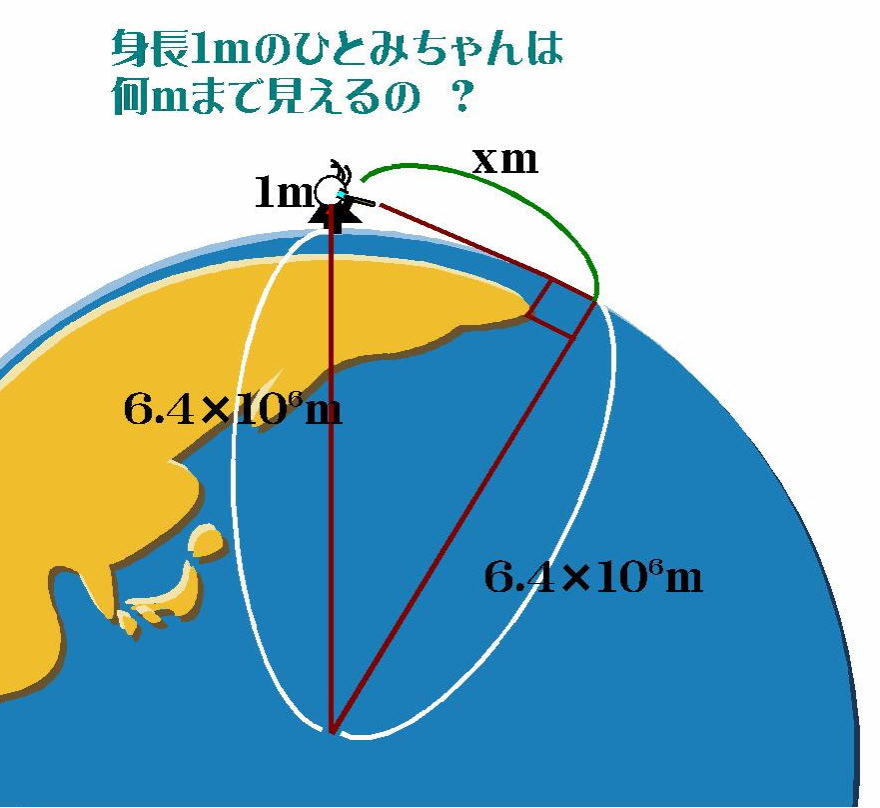
地球は半径6.4✕103km（6.4×106m）の完全な球で、ひとみちゃんの「瞳」は北極点の真上、1mにあり何の障害もなく見ることが出来たとします。
三平方の定理から、(6.4✕106+1)2=(6.4✕106)2+X2
∴ X2=(6.4✕106+1)2-(6.4✕106)2=(6.4✕106)2＋2✕(6.4✕106+1)✕1+1-(6.4✕106)2=12.8✕106+1
∴X≒103√12.8=3.577✕103m 答え 約3600m
ところで、上のような3600mもの長さを測れる物差しと、分度器+三角関数表があれば、今度は地球の半径が求められます。
プトレマイオス(AD90年頃～AD168年頃)は、「弦の数表」（三角関数表）をすでに持ってい（たのは事実）で、地球の半径を求めていたのではないか？といわれています。（そうではないという人もあり）
その原理は上の図を再び用います。
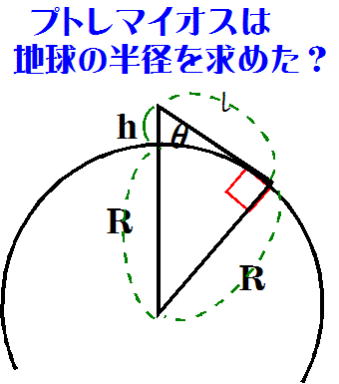
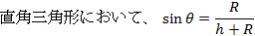
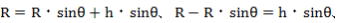
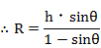
つまり、ひとみちゃんが水平方向から視線を下向きに何度傾けて地の果てを眺めたか、その角度を90°から引いた値がθとなり、なんと地球の半径が求められる－というファンタスチックな計算式なのです。
measure、climb、shadow、method、difficult、principle、fan、be in proportion、be related to～、
relationship(n),relation(n)、the meridian、latitude、longitude、north pole（south pole）、
the summer solstice(the winter solstice)、Vernal Equinox Day、Autumn Equinox Day、cliff、
volcano、ploblem、element、vertical、horizontal、explanation、incline to～、angle、direction、
observe、figure、height、danger、dominate、hold sway、power station、turtle、elephant、
planet、the Copernican theory、the Ptolemaic theory
