遠眼鏡（江戸時代） 　遠眼鏡の筒は和紙を重ねて貼り、漆（うるし）を 塗って堅く壊れないように強度を高めました。これ を一閑張（いっかんばり）というのだそうです。 上野・国立科学科学博物館で撮影	M－v ロケット 　1997年～2006年運用。全長30.7m、直径2.5 m、重量139トン、打ち上げ能力1.8トン。7回の 打ち上げを行い6回成功しています。世界最大の固 体燃料ロケット。 相模原　JAXA宇宙航空研究開発機構で撮影

　恒星の世界では星の明るさ（等級）、放射エネルギー、星の質量と光度の関係、恒星として輝いている時間の長さなど「星の物理」にかかる事項について多くのことを学びます。

　しかし逆に私たち人類は、あるいは地球はどのように生まれてきたのか、そしてどこへ向かっていくのかというきわめて思弁的な世界に私たちを向かわせるような単元になるのではないでしょうか。
　
　たしかに、古生物の単元、あるいは太陽系誕生の単元では「なるほど、こうして地球が誕生して、生命が現れたのね」そのような「確認」のような理解だったのが、恒星の世界や宇宙を学ぶことに至っては、「宇宙の始まり」という根源的な崖に立たされる思いをするからではないでしょうか。

　宇宙船地球号－私たちはどこからきてどこへ行くのでしょう。

 

　恒星の世界に出てくる数値、公式（既習事項）
　1AU（1天文単位）＝地球～太陽間の平均距離　1.496×10⁸km(これまで1.5×10⁸km、「No.28　地球・惑星の公転」、

　「No.30　ケプラーの法則」で既出)

　d=3.26/P（光年）＝1/P（PC）1光年＝9.46×10¹²km(「No.28　地球・惑星の公転」で既出)

 

 

ヒッパルコス像（田近英一　惑星・ 太陽の大発見（新星出版社）より 借用　一部改変）

19Cハーシェルが「等級」の概念を提唱、ポグソン （後にポグソンの公式が出てきます）によって確立 されます。　BC130年頃ヒッパルコスが空に輝く11 00個ほど恒星について、最も明るい星を1等星、最 も暗い星を6等星として分けました。　明るさの差 ＝「光比」が、1等差で5√100=2.51倍、5等差で 100倍の差があることが分かっています。

　星の明るさは、6等星の光度を1とすると5等星の明るさは、6等星の5√100=2.51倍。４等星の明るさは、5等星の⁵√100=2.51倍。3等星の明るさは・・・。となって、等比数列になっていることが分かります。

　表-1

 

　1等星の明るさをl1、2等星の明るさをl2とします。明るさの比較をすると、

 

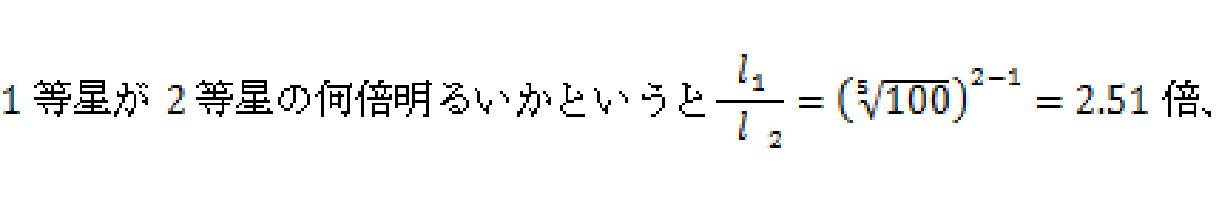
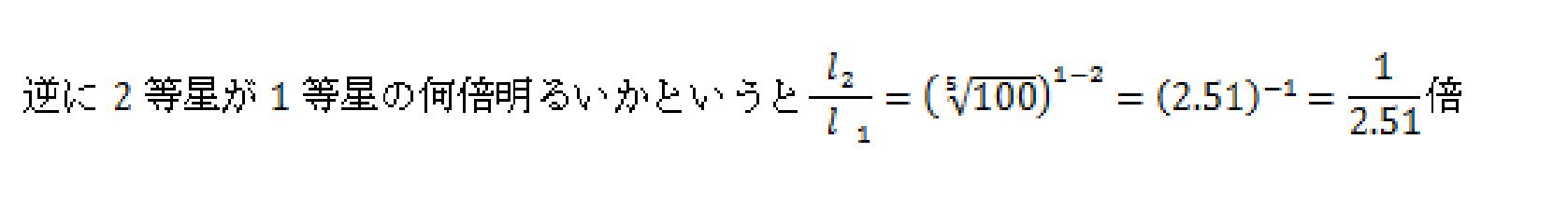
　一般にm等星の明るさをlm、n等星の明るさをlnとすると

 

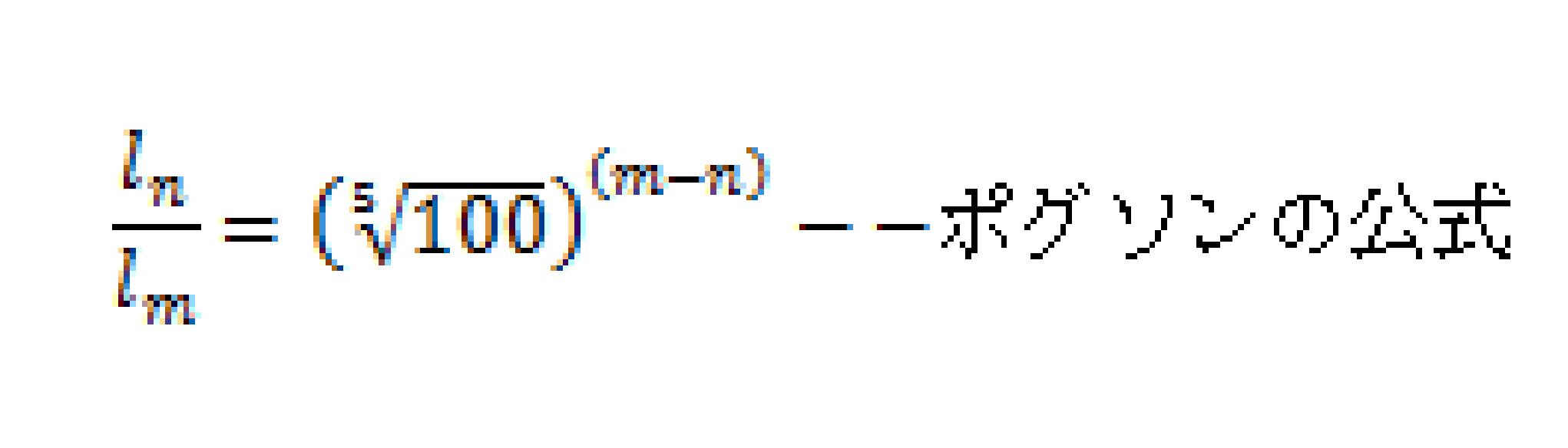
　ポグソンの公式、d=3.26/P（光年）＝1/P（PC）の公式を使う問題

　Q１　年周視差0.40秒の恒星の距離は何光年か？また何PCか？

　【解答】

　d=3.26/P より

　d=3.26/0.40=8.15光年、

　またd=1/P よりd=1/0.40=2.5PC

 

　Q2 　(1) 3等星と6等星ではどちらが何倍明るいか？(有効数字3桁)（⁵√100=2.51）

　　　　(2) -1等星は11等星の何倍明るいか。(有効数字3桁)（⁵√100)2=6.30）

　【解答】

　　(1)

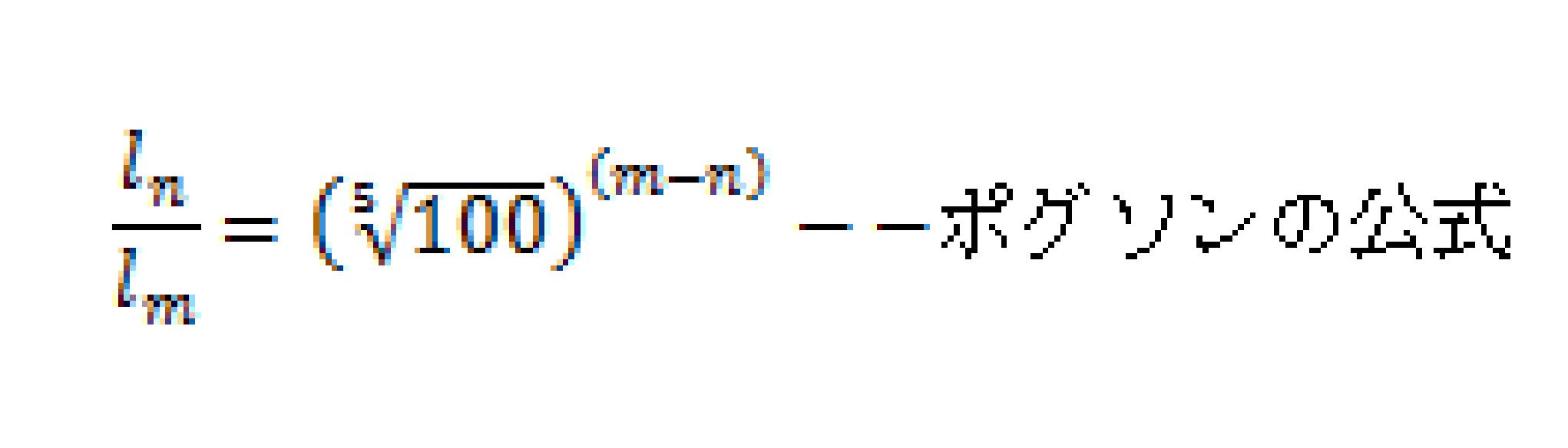
　より

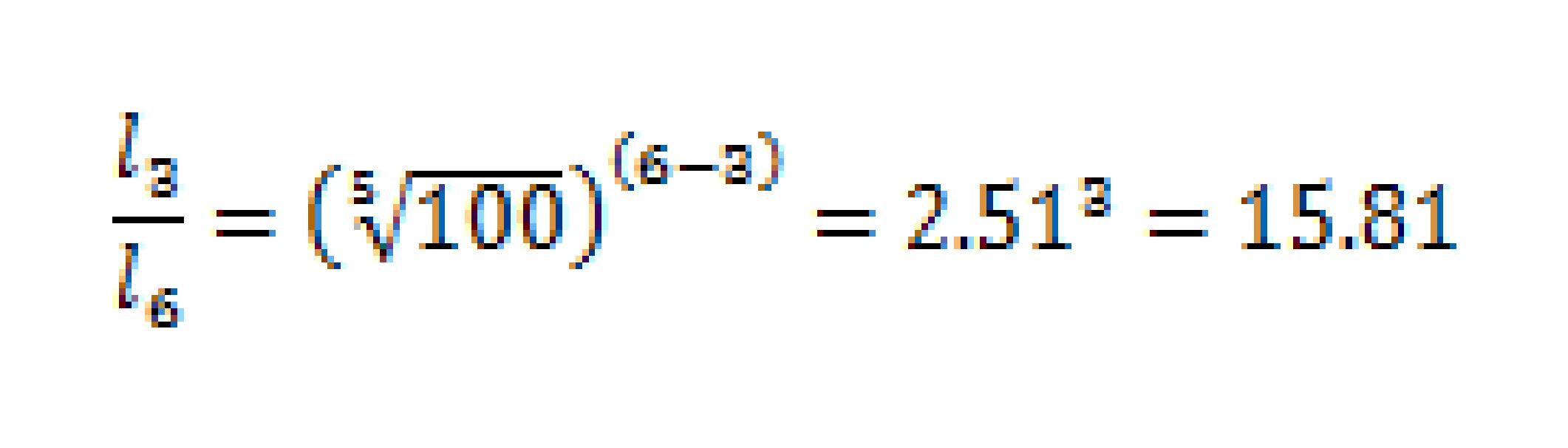
　答え　3等星の星が6等星の星より15.8倍明るい

　（２）

 

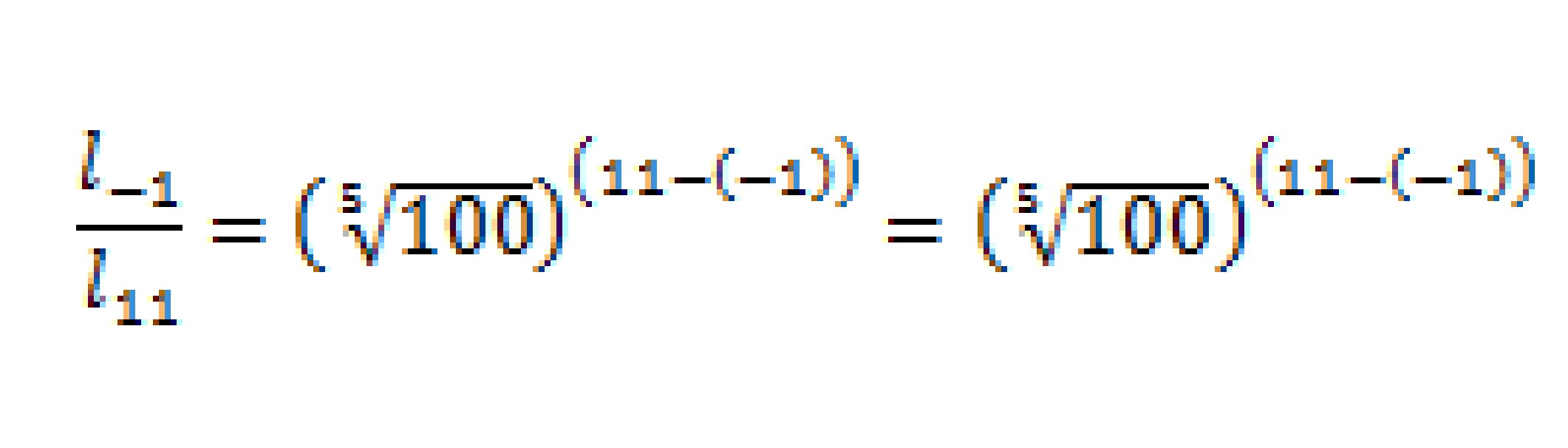
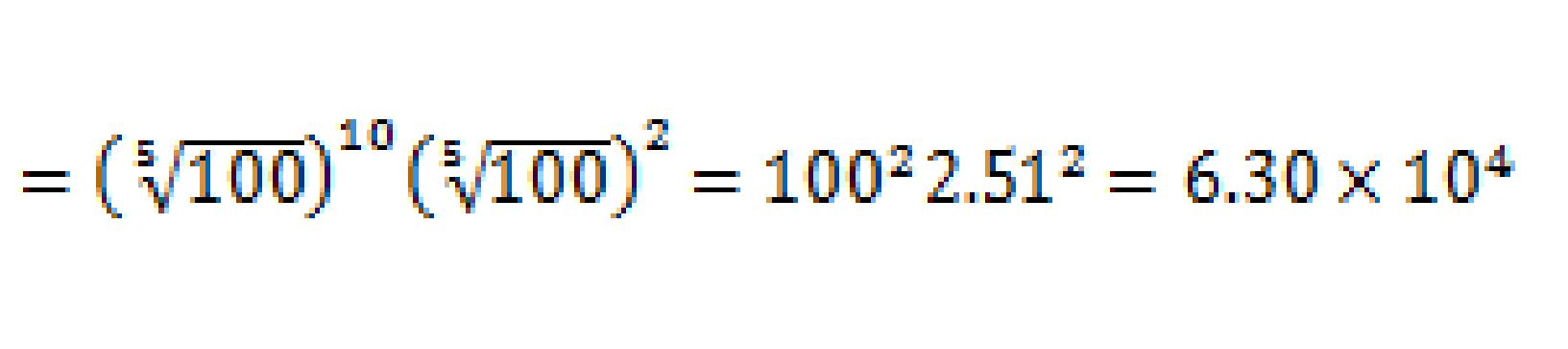
　答え　-1等星の星は11等星の星の6.30×10⁴倍明るい

 

 

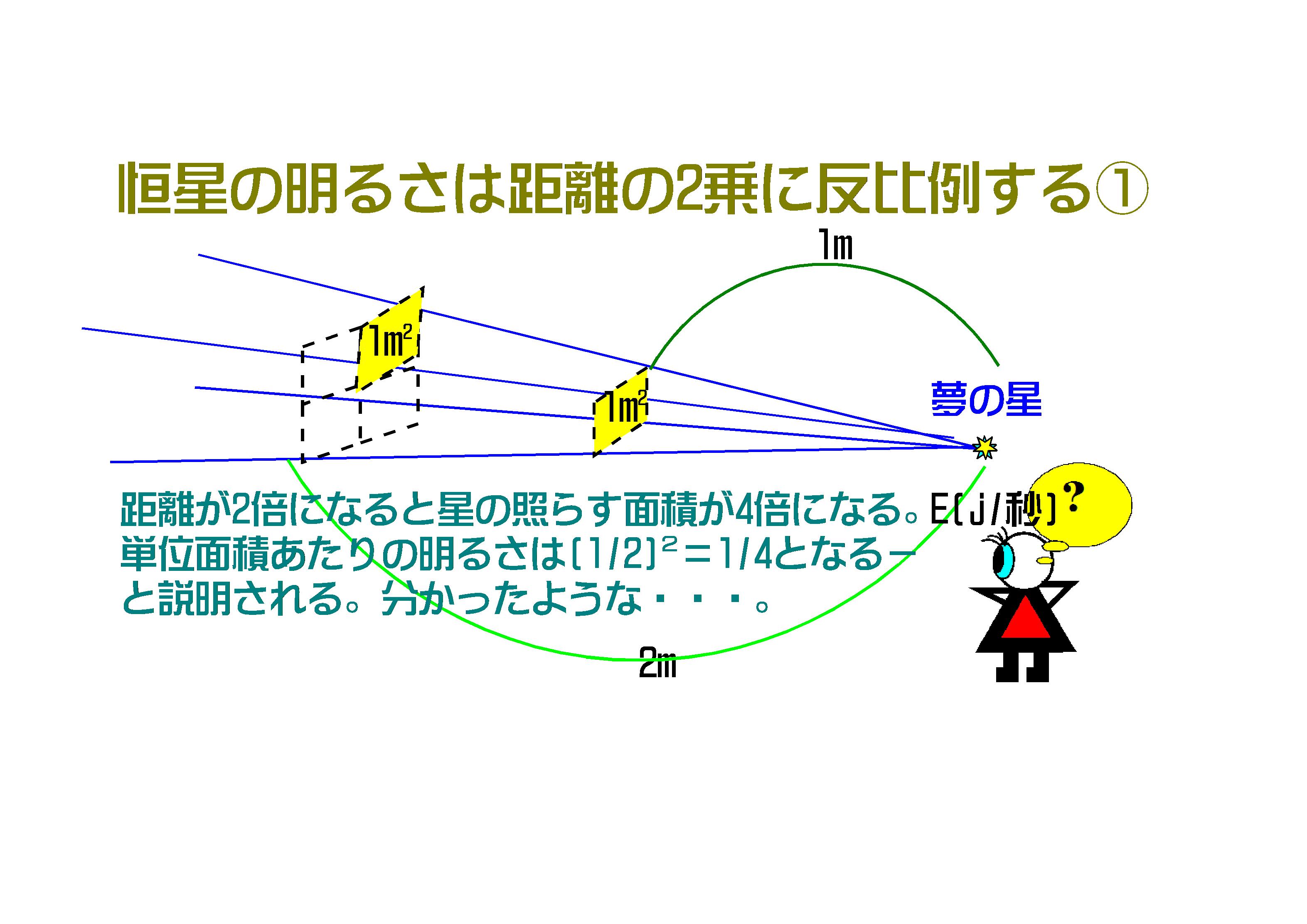
　図－１

　「夢の星」から（十方世界に）毎秒Ejのエネルギー（光）が放射されているとして、光に垂直な1ｍ²の平面が受け取る「星の明るさは、距離の二乗に反比例する」と言われるのですが…。

　金科玉条のように唱えて、何か分かったような、それでいて分からないような。
　　
　でも、このことは「No.17　太陽からのエネルギー供給、熱収支」1　太陽定数の２枚の図に考え方が示されていました。

　太陽定数＝「1.5億km離れた太陽からどれくらいの暖かさ、明るさを頂いているか」表した値。

　Cal(カロリー)表示をしたり、W(ワット)表示をしたり学習指導要領の改正によって変化しています。

　近年は1.366✕10^３W/m^２のW表示のようです。cal表示では2.0cal/cm^２・min

　太陽に近い水星では太陽定数は大きくなって「太陽は明るく見え」、太陽から遠い土星では「暗く見える」ことになります。これは普段街灯が近くにあると明るく、遠いと暗く見えるのと同じことになります。

 

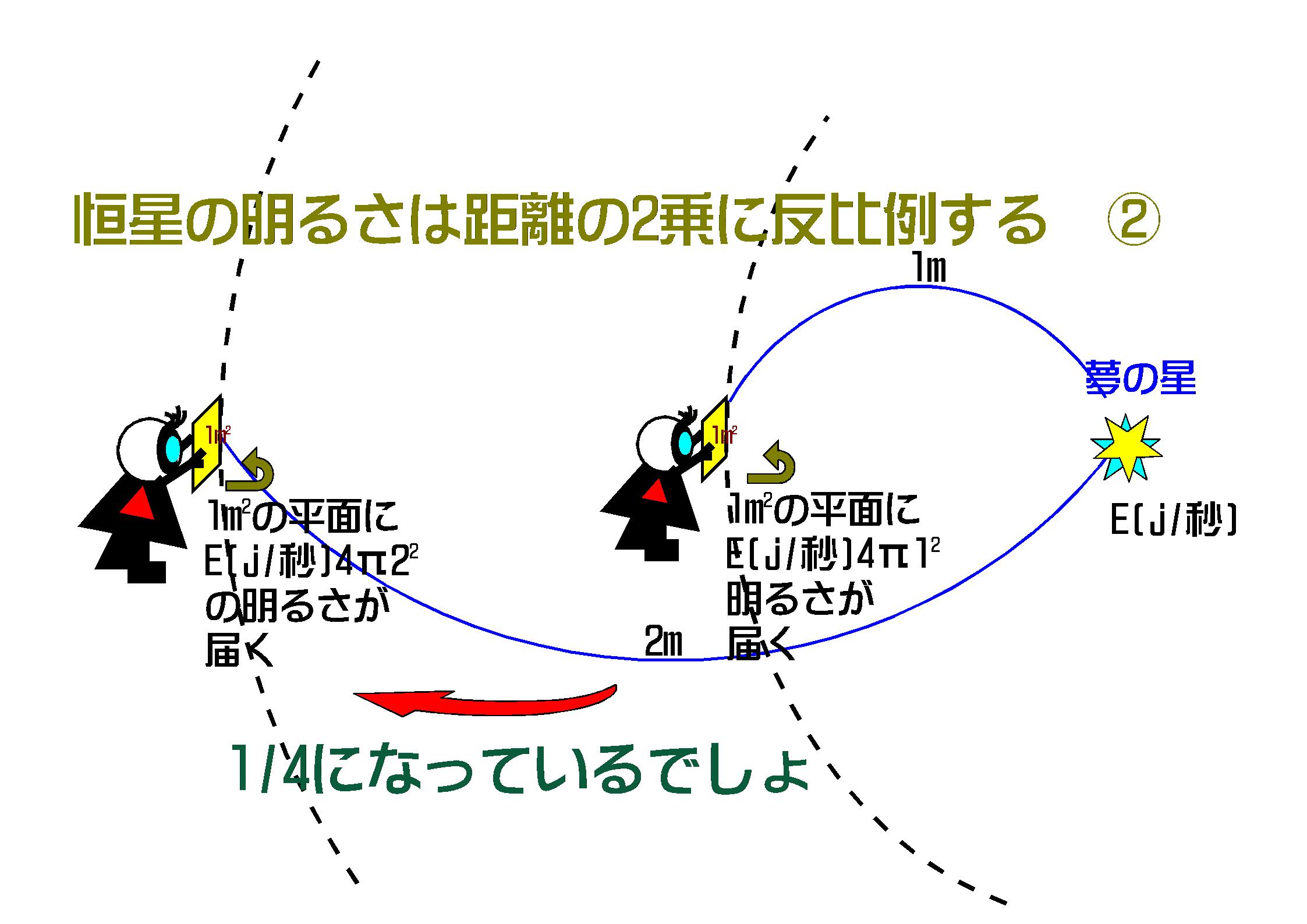
　図－2

　上の図は「夢の星」から放射される明るさ（エネルギーE(J)）が、くまなく・等しく1m²の平面（球面）に分配されることを説明しています。
　球(球の半径＝r)の面積(S)の公式は「S=4πｒ^２（心配ある事情）」でした。ですから1m²あたりにはEを4πｒ^２で割ればよいことになります。

　図－２の計算式は見にくいので説明しますと、
　夢の星から1m離れたところで1m²の平面に分配される星の明るさは、「放射エネルギー÷半径1mで作った球の面積」ですから

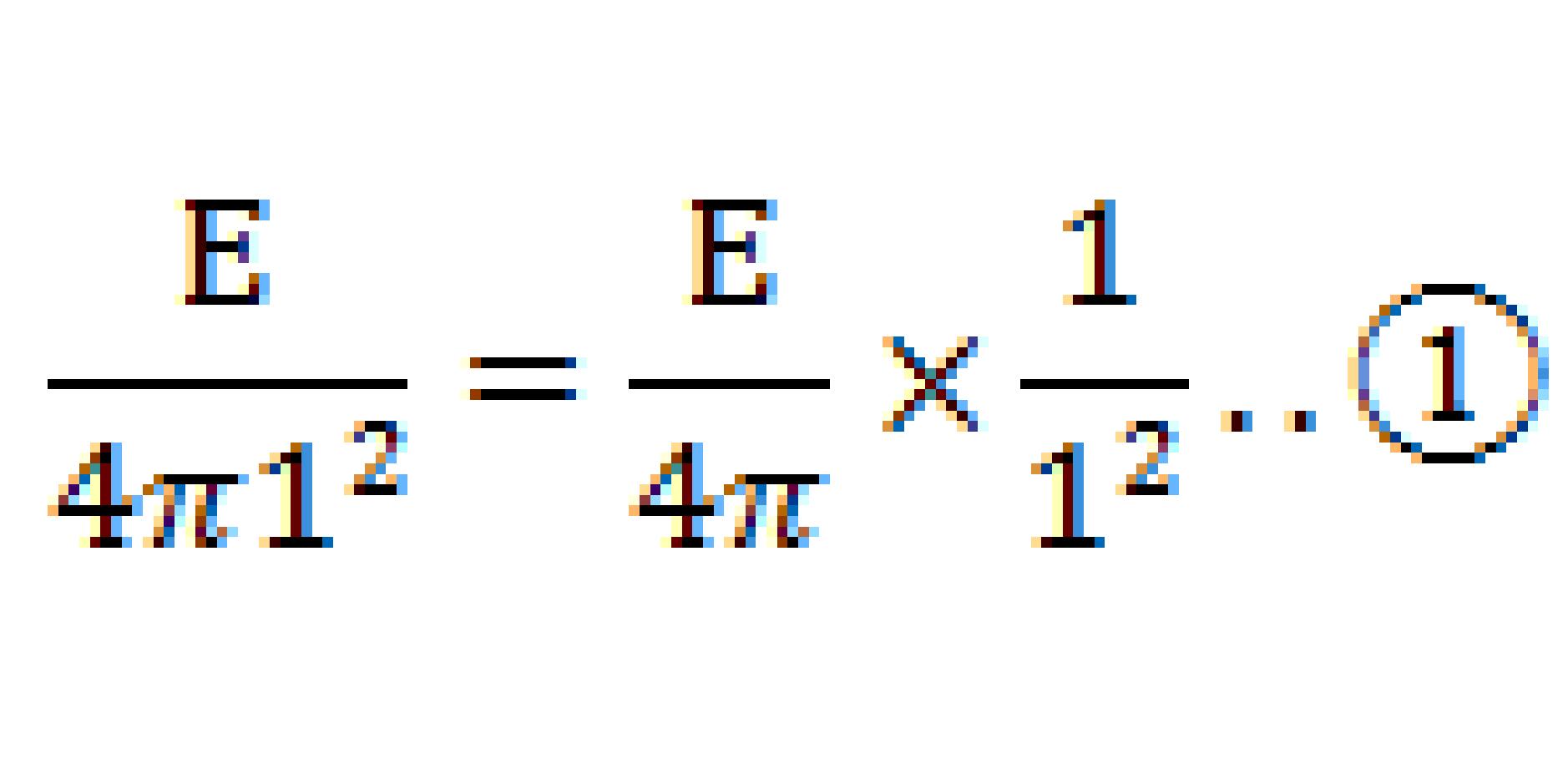
　同様に夢の星から2m離れたところで1m²の平面には

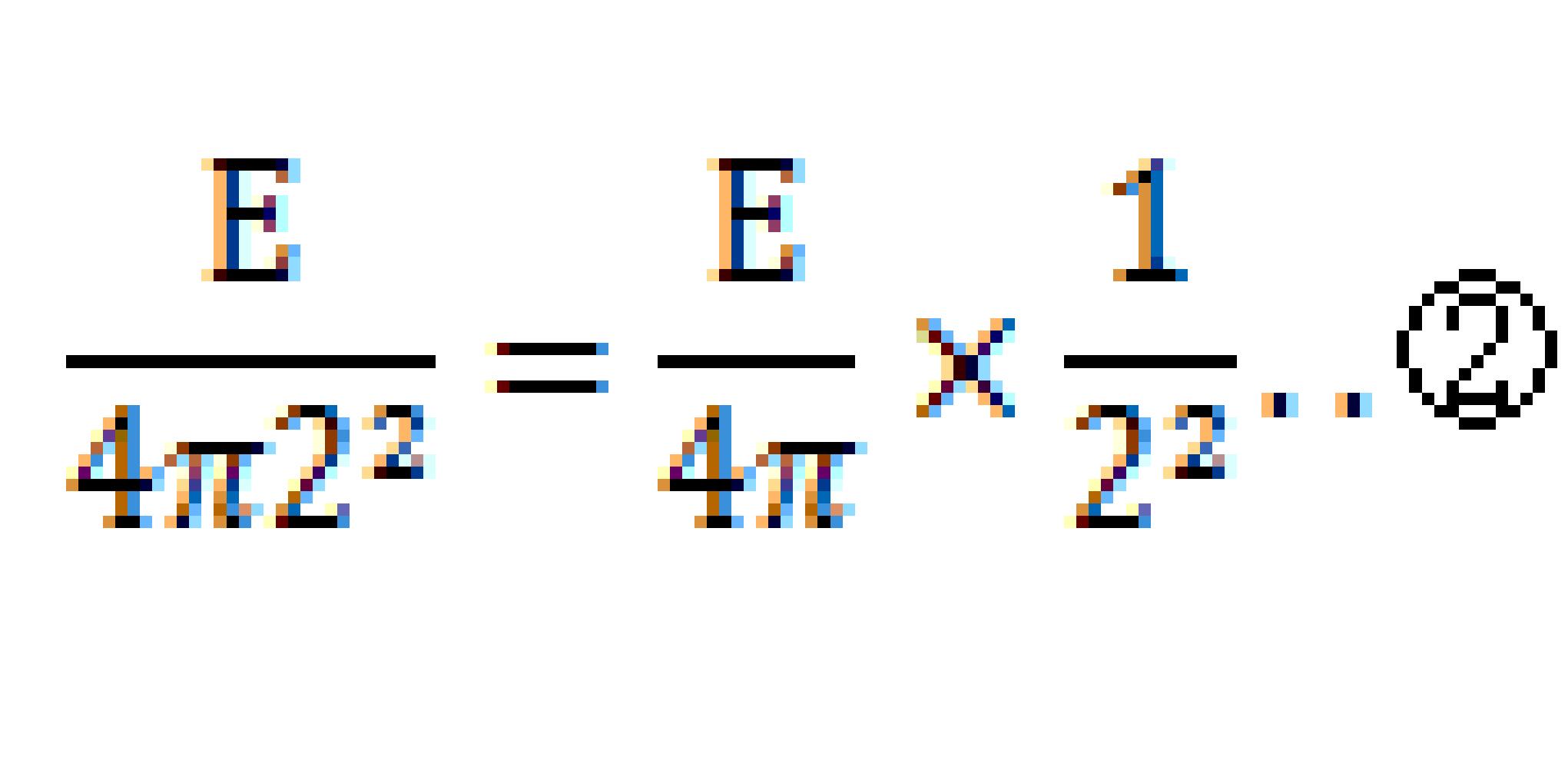
となって「恒星の明るさは距離の二乗に反比例する」ことが分かります。

 

 

 

　

　図－3

　図－４

　太陽は1.5億kmと、私たちの感覚からすれば十分遠いですね。

　それで実視等級は－26.8等と圧倒的な明るさです。ところが10PC(32.6光年、これもまた気の遠くなるくらい遠い距離なのですが)まで離れると、太陽は4.8等と「ふつうの星（巨人の星までいかないんです）」なんです。

 

　

　この公式を用いる計算問題は頻出です。どのように公式が導かれるか見てみましょう。

　dPCの距離にある星がm等星に見えたとします。（実視等級：m等）そのときの明るさをℓmとすると、ℓm＝1/d²・k（kは比例定数、星の明るさは距離(d)の2乗に反比例しました。）

　一方、その星が10PCの距離にあるときは絶対等級はMで表されますし、そのときの明るさはℓM=1/10²・ｋ　となります。

　明るさの比をとると

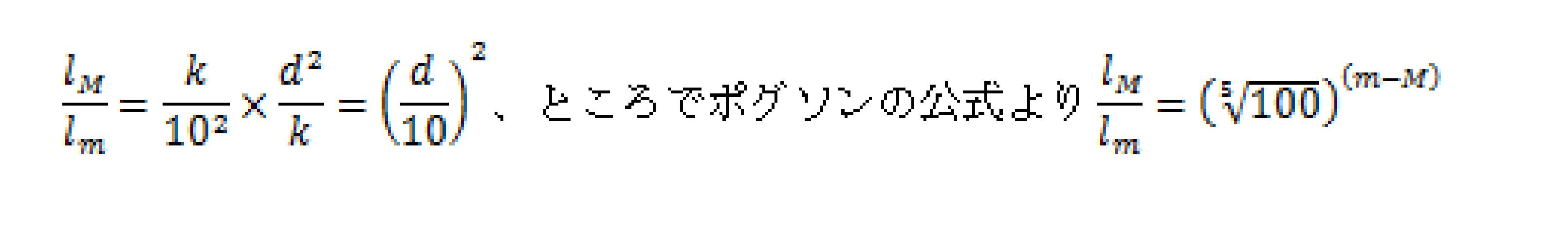
　両辺を常用対数にとると

 

 

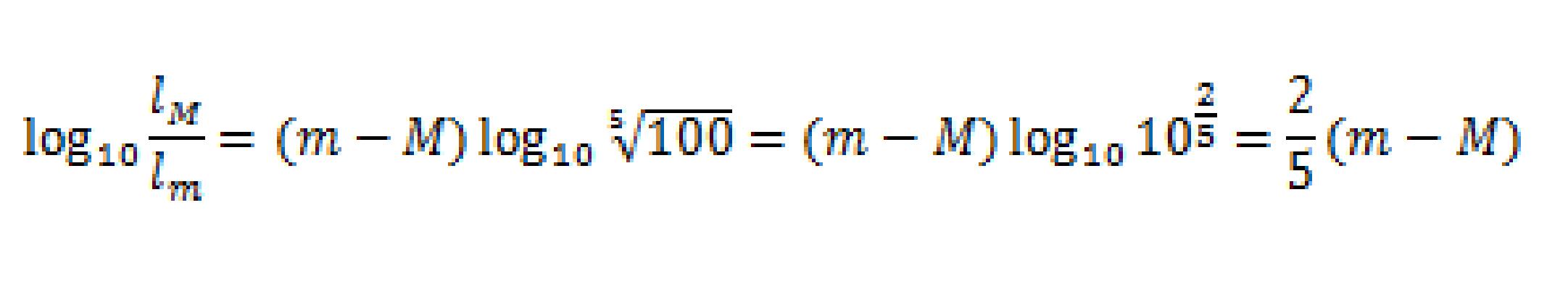
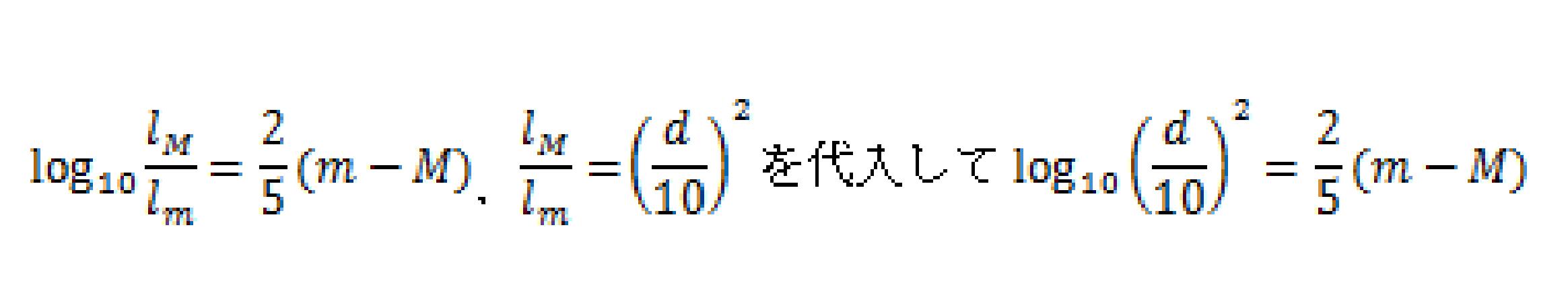
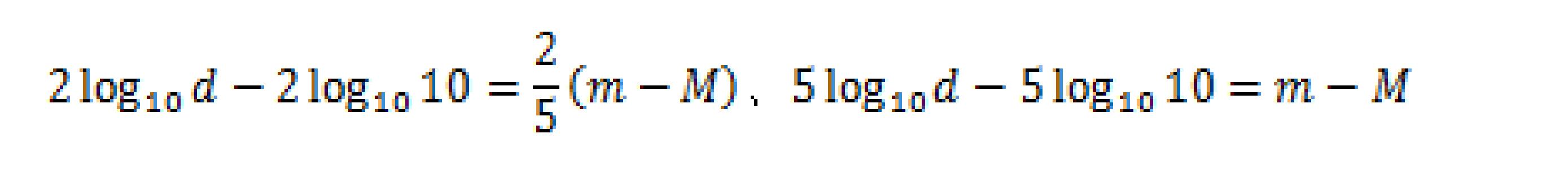
　距離指数の公式

 

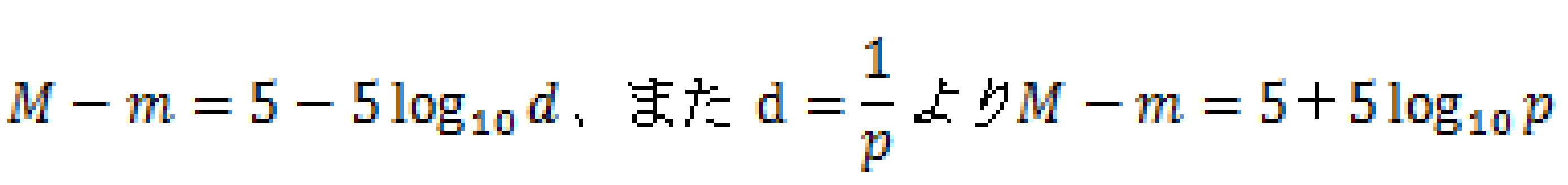
　Q１　ある星の距離が1000PC、実視等級が+5等である。絶対等級を求めよ。

　A1　M-m=5-5log₁₀dより、M-5=5-5log₁₀10³、M=5+5-15=-5　答え　絶対等級－５等

 

　Q2　絶対等級+13等、実視等級+8等である。この恒星の距離は何PCか。また、何光年の距離か。

　A2　M-m=5-5log₁₀dより、１３－８＝5-5log₁₀、０＝-5log_1０d、∴d=10⁰=1PC、3.26光年

 

　Q3　実視等級＋6.2等、距離5.0PCの恒星の絶対等級を求めよ。ただし、必要な場合、log₁₀2.0=0.40として計算、有効数字2桁で　　　求めよ。

　　　公式に直接当てはめれば解ける-そういう問題ではなくて、対数の公式操作も問われます。

　A3　M-m=5-5log₁₀dより、Ｍ－6.2＝5-5log₁₀10/2、Ｍ＝5+6.2-5（log₁₀10-log₁₀2）、Ｍ＝11.2-5（1-0.40）＝+8.2等

 

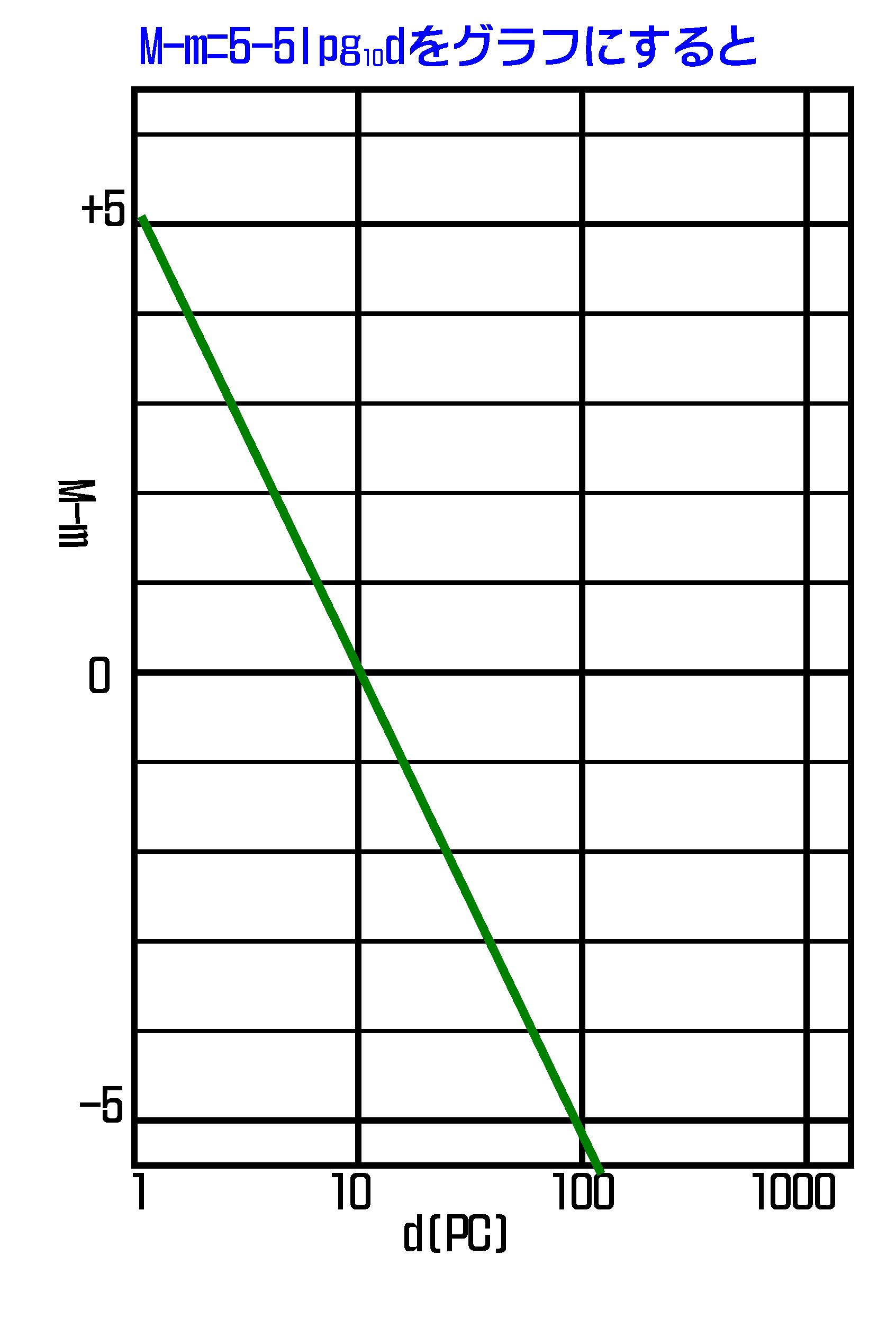
　図－５

　M-m=5-5log ₁₀d の式で、dに d=1=10⁰、d=10=10¹、d=100=10² 、 d=1000=10³ 代入すればM-mの値がそれぞれ求められます。

　M-mの値を縦軸に、d(PC)の値を横軸にとって描いたのが図－５になります（片対数目盛になっています。図－５のタイトルのlogが「lpg」になってました・・・。）。

　たとえば図－５に関わる問題はこのような出題になります。

　①　ウオルフ359星の実視等級は＋13.5等、年周視差は0.41秒である。図－５を用いて絶対等級を求めよ。

　②　太陽（絶対等級＋4.8等）はウオルフ359星の10⁴倍以上明るいか、否か。

【解答】
　①　距離指数の公式を用いて解こうとしても、log₁₀0.41 、log_1０2.40の値が示されていませんから解くことができません。

　　d=1/pよりd=1/0.41=2.4PC、 図－５（下図）よりM-m＝+2.7と読み取れます。M-m=M-13.5=2.7、M=16.2等- 答

　②

 

 

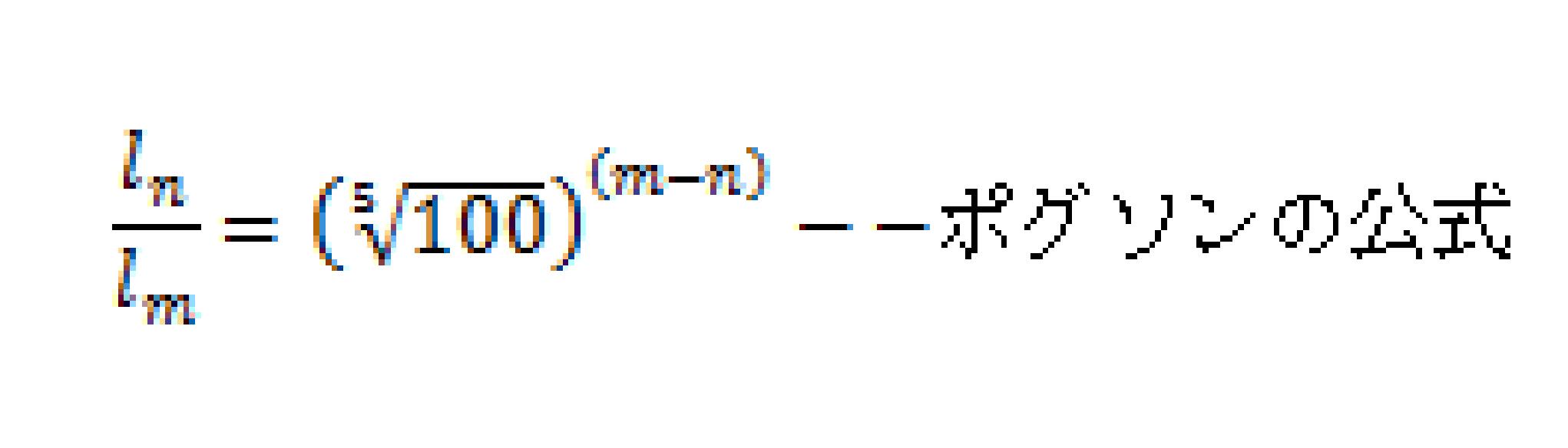
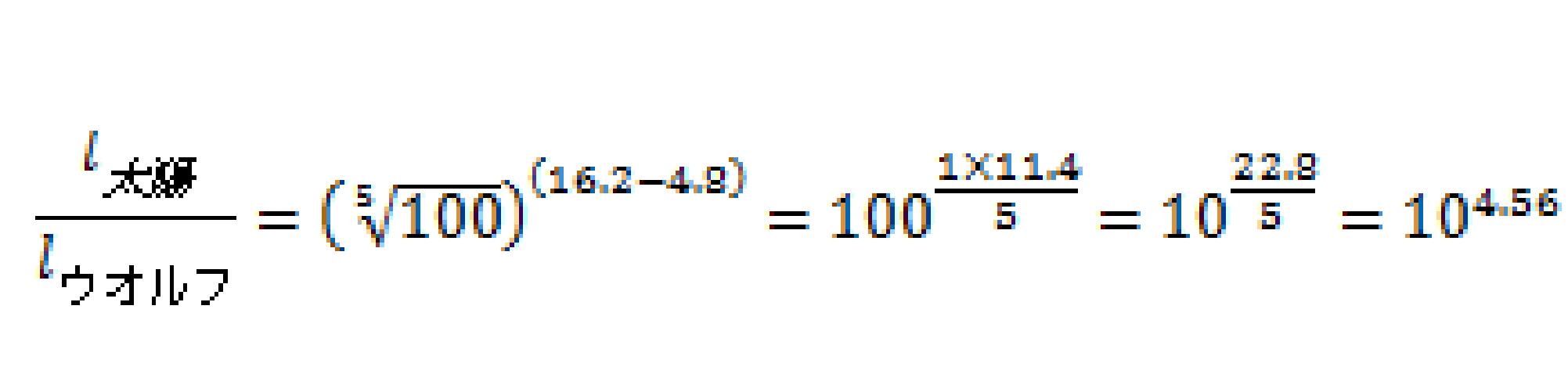
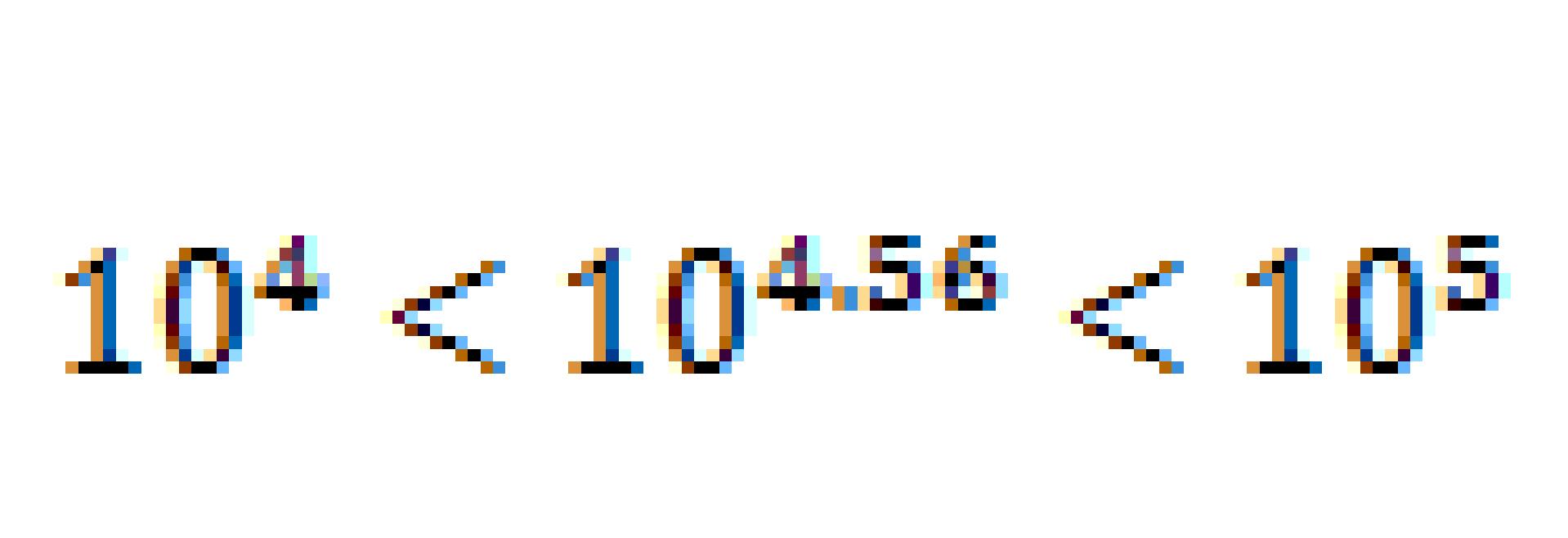
　答え　太陽は10⁴倍以上明るい

 

恒星	実視等級	絶対等級
A	３．７	５．９
B	０．３	４．７
C	１．０	２．４
D	１．６	－０．１
E	１．２	－３．２

　上のようにA～E、五つの恒星の実視等級、絶対等級が測定されたものとする。以下の問に答えよ。

問1　最も明るい恒星はどれか。

問2　32.6光年より遠くにある恒星をすべて答えよ。

問3　地球に最も近い恒星、地球から最も遠い恒星はどれか、答えよ。


【解答】
問1　恒星を同じ距離に並べた時の明るさで決めればよいわけですから、絶対等級の最も小さい恒　星が最も明るいことになります。
　したがって、答え－E星

問2　絶対等級を決める距離は、32.6光年＝10PCでした。したがって、M－m＝5－5log₁₀10、
　M－m＜0　を満たせば10PC以上の距離にある恒星になります。
　上の説明ですっきりしない場合は図を描くといいでしょう。

　たとえばA星の場合

問3　この問題も問2と同様にM－m＝5－5log₁₀d で考えます。
　dが小→M－mは大、dが大→M－mは小となります。恒星A～EについてM－mを計算すると次のようになります。

恒星	実視等級(m)	絶対等級(M)	M-m
A	３．７	５．９	2.2
B	０．３	４．７	4.4
C	１．０	２．４	1.4
D	１．６	－０．１	-1.7
E	１．２	－３．２	-4.4

　したがって
　地球に最も近い星はB星、地球から最も遠い星はE星－答え

 

 

　イタリアの天文学者アンジェロ・セッキ（Pietro Angelo Secchi、1818～1878）が1860年代後半、恒星をグループ化する一つの方法として、「色」と「スペクトル線の見え方」によって四つのグループに分類したのが始まりです。

　「スペクトル線の見え方」の違いは、恒星の「化学組成」の違いではなく恒星の「表面温度の違い」から原子・分子・イオンの状態の変化を示すものと理解されるようになりました。

　恒星の温度の高い方からスペクトル型はO(45000K)-B(29000K)-A-F-G(6000K)-(R-N)--K-(S)-M(3900K：絶対温度)と分類されました。

　セッキの恒星の「色」と「スペクトル線の見え方」による分類法はアメリカのヘンリー・ドレイパー（Henry Draper　1837～1882　医師・天文学者）が引きつぎ、かれは22万以上の恒星について分類を行いました。この研究にはハーバード大学天文台長ピッカリングのほか、三名の女性天文学者が参加したと言われています。

　分類の結果は「ヘンリー・ドレイパー・カタログ」として1918～1924年出版公表されました。このカタログによって星をスペクトルで分類する系統的な研究が始まりました。
　
　アイナー・ヘルツシュプルング （デンマーク　Ejnar Hertzsprung 1873～1967）そしてヘンリー・ノリス・ラッセル（アメリカHenry Norris Russell、1877～1957）は、恒星の絶対等級を縦軸に、スペクトル型（表面温度）を横軸にとった「恒星の分布図」をそれぞれ、独立して提案しました。

　二人は共同研究を行ったのではありませんでしたが、提案された「恒星の分布図」は二人の名前の頭文字をとって「HR図（HR Diagram）」（ヘルツシュプルング・ラッセル図）とよばれるようになりました。

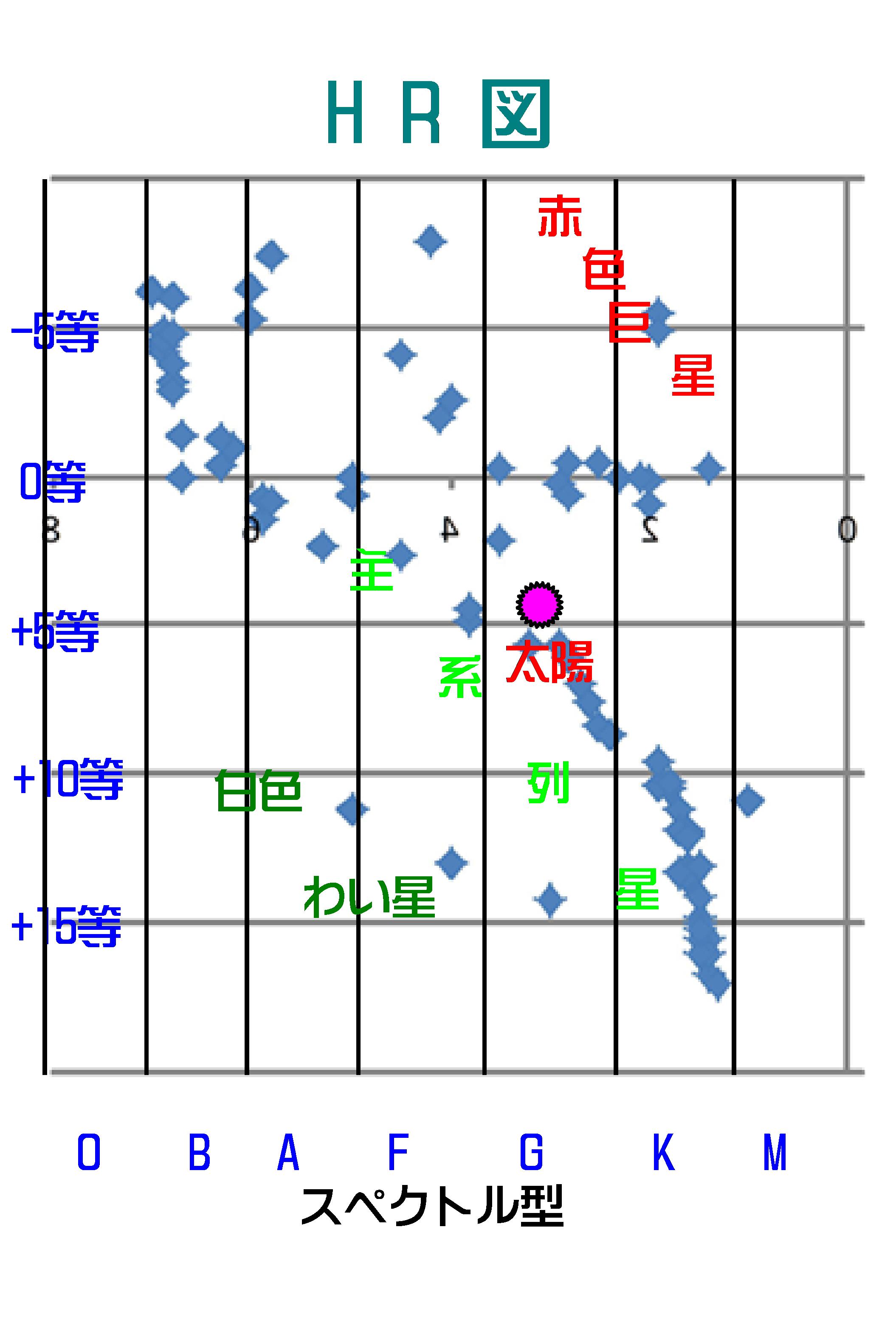
　図－６

　図－６において重要なことがあります。たとえば、スペクトル型K(表面温度が絶対温度T(K))の恒星で+15等星と+10等星の二つの恒星があったとします。このふたつの恒星の半径はどのような関係になるでしょうか。

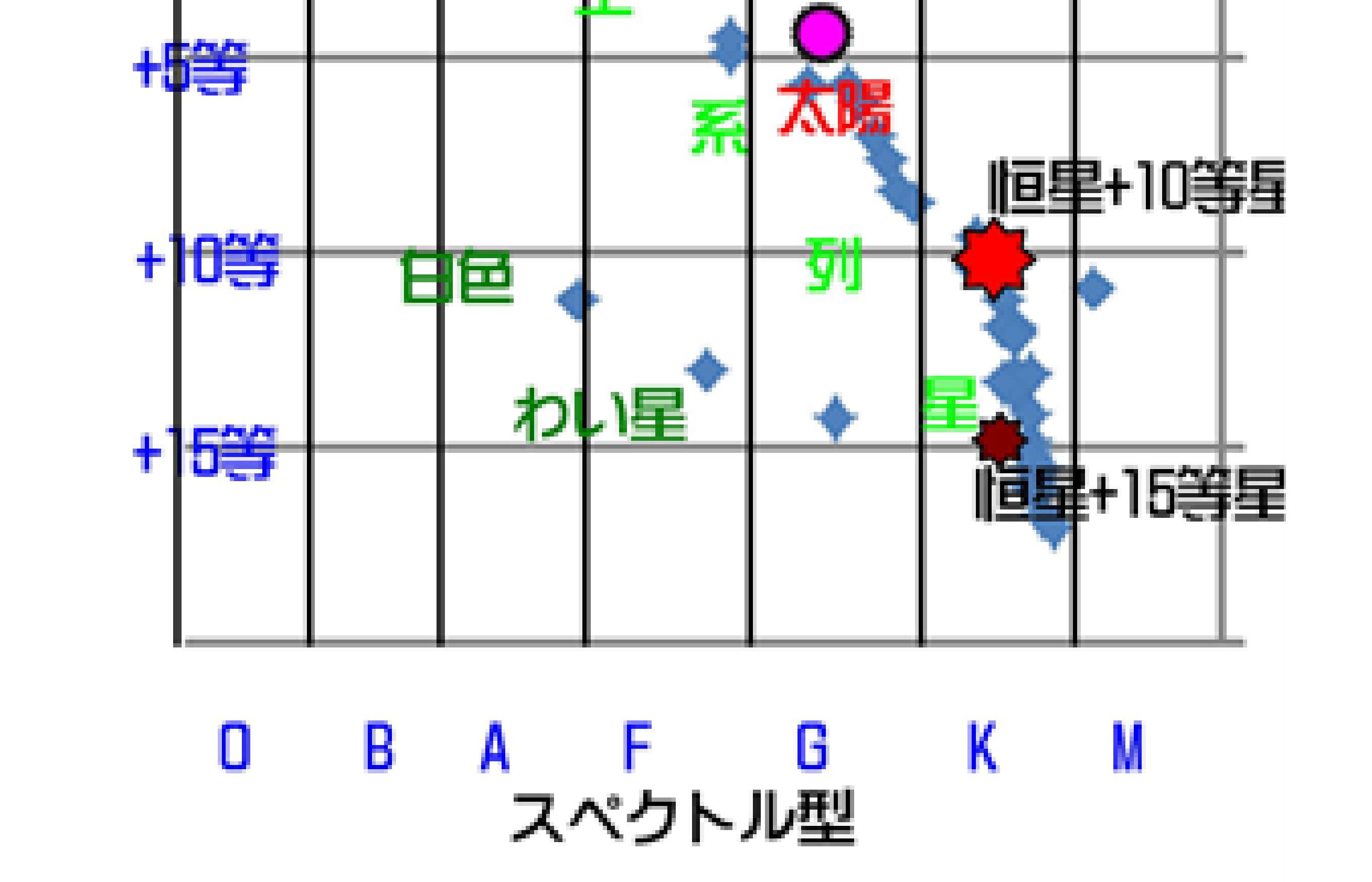
　図－７

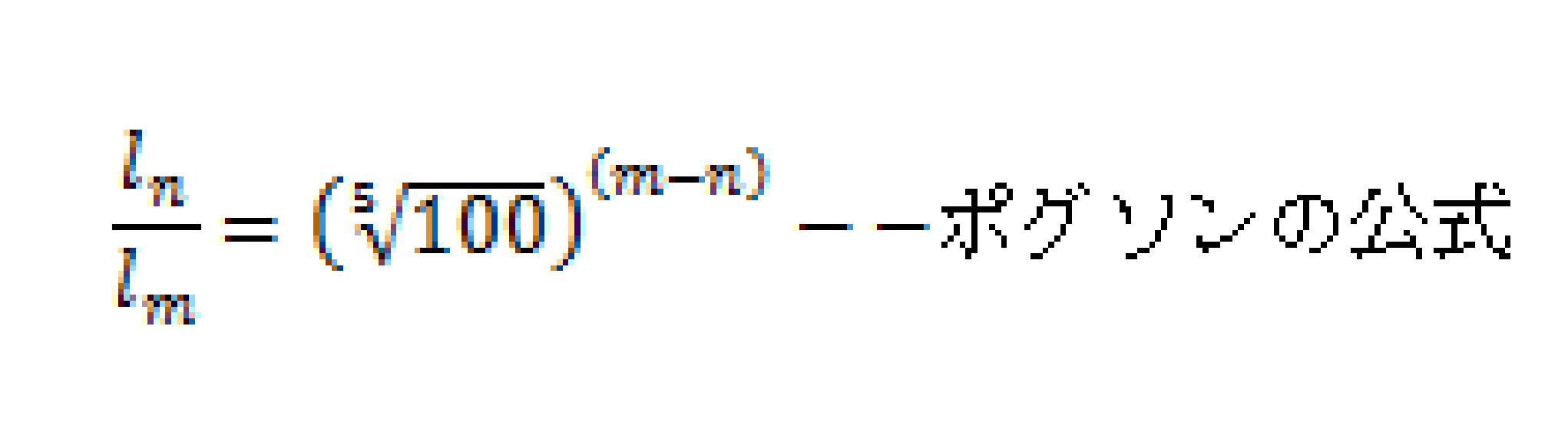
　より恒星+10等星の明るさは恒星+15等星の明るさの

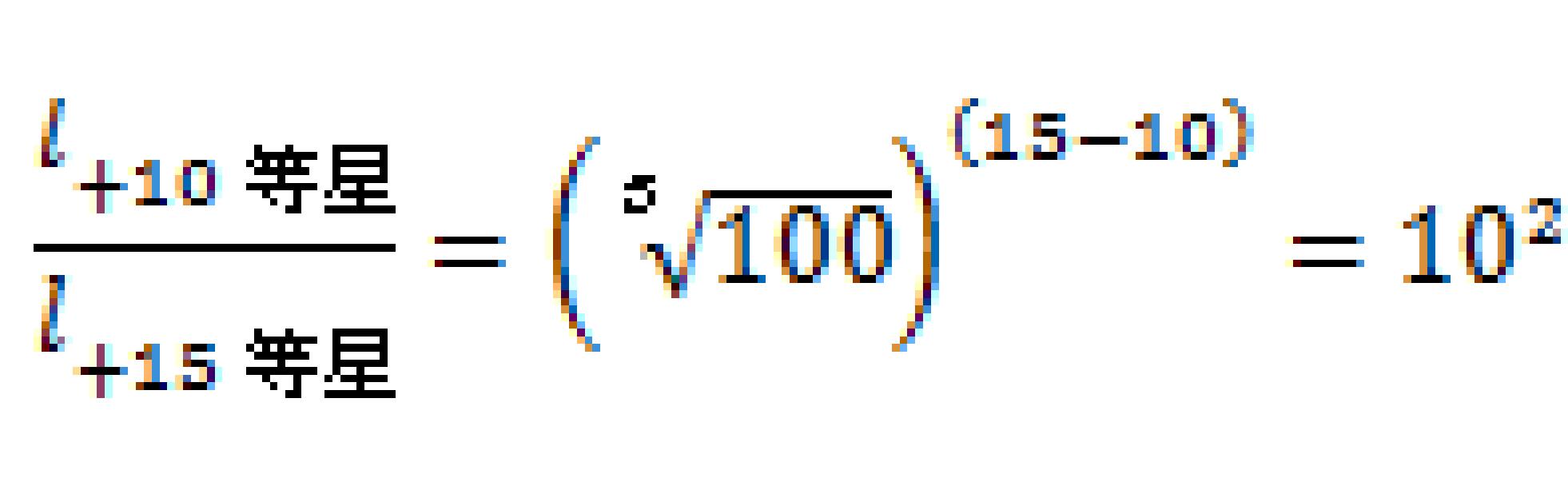
　倍となります。

　一方、恒星の表面から放射されるエネルギー（明るさは）

　「恒星の表面積」×「シュテファン・ボルツマンの式」＝4πR^２×σT⁴でしたから

 

　二つの恒星の半径の比は

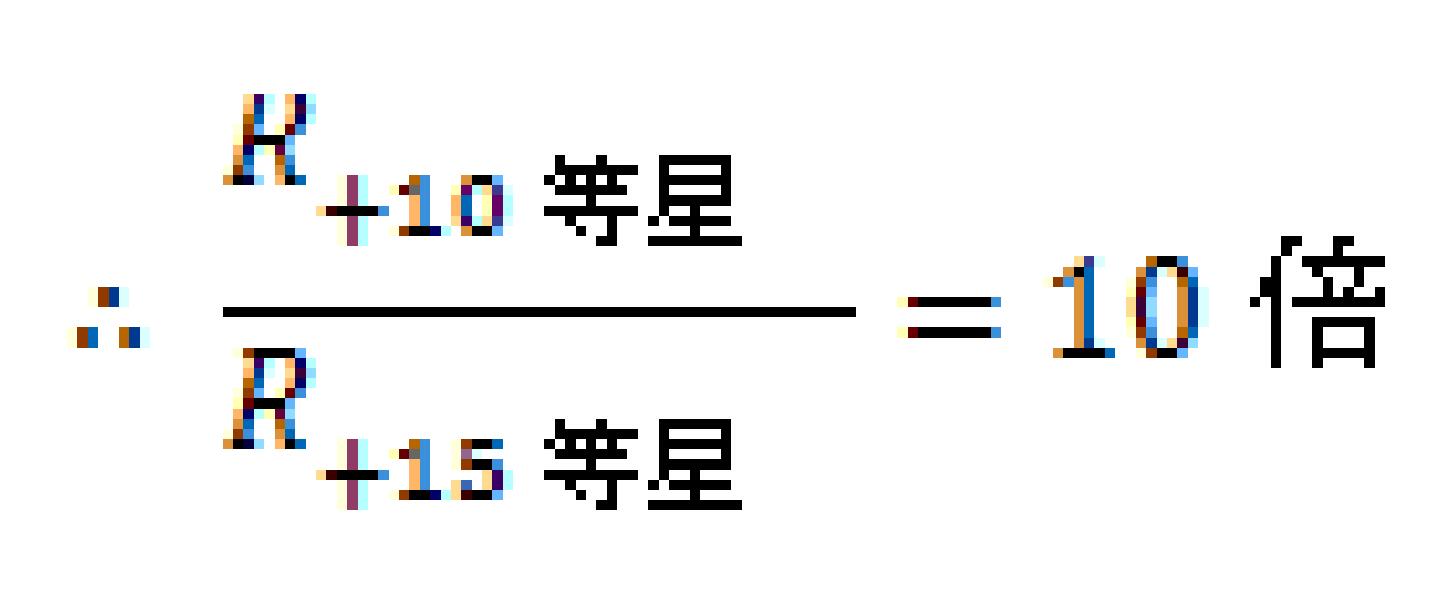
　となります。

　つまり「HR図上で、温度が等しくて5等差の光度差があれば恒星の半径は10倍異なる」ことになります。

　このようなわけで、HR図上では恒星の半径の大まかな大きさが分かることになります。それ故星の色が赤くて大きい星は「赤色巨星」、温度が高く青白く小さな星は「白色矮（わい）星」と分類されることになります。太陽の半径を1太陽半径とすると、およそ図－８に示されるような関係になります。

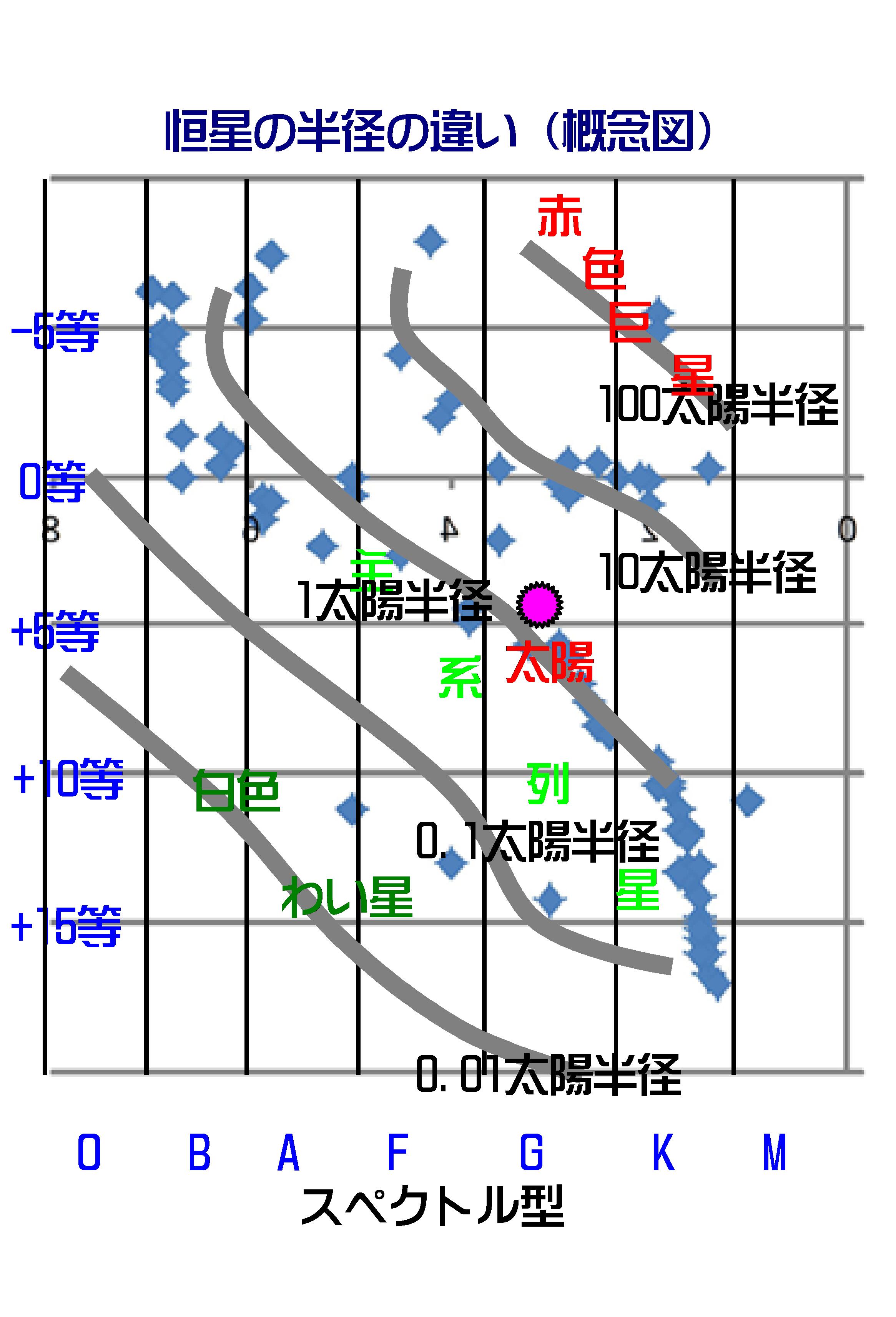
　図－８

　

　図－６について詳しくは説明しませんでしたが、やっとここで「巨星」、「矮（わい）星」について説明できます。

「主系列星」：

　HR図上で、左上から右下に帯状に並んでいる恒星。

「巨星」：

　HR図スペクトル型G、K、Mと低温で、したがって「黄色」～「オレンジ色」～「赤色」に見え、太陽の半径の100倍程度の恒星。太陽の半径の100倍以上の巨星は「超巨星」。密度は10^-3～10^-6g/cm³とスカスカ。（太陽の平均密度は1.4g/cm³でした。）

「白色矮星」：

　HR図スペクトル型B、A、F型で、絶対等級が+10等以上と「青白」～「白」色の暗い恒星。密度が、10⁵g/cm³と非常に高いのが特徴。

　「密度＝質量÷体積」でしたね。たとえば「図－８」において「0.01太陽半径」の説明文字があり、1太陽質量程度の矮星（スペクトル型は何でもかまいません）があったとします。その矮星の密度は、密度＝1太陽質量÷4π(0.01太陽半径)³/3　太陽の密度の10⁶倍になることが容易に計算できます。

　このようなことからも矮星の密度が非常に大きいことが分かります。

　図－９

　分光視差：図－９はすでに「M-m=5-5log ₁₀d の式をグラフにあらわすと」として,図－５で示していました。

　まず、ある恒星を観測します。するとその恒星の実視等級(m)、そして吸収線の見え方の違いから巨星、主系列星、矮星の区別がつきます。そうすると、HR図からその恒星のおよその絶対等級(M)が推定できます。

　そうなると図－９からその恒星のおよその距離 d （年周視差 p）が推定できます。（d=1/p 年周視差) 　

　このようにして得られた年周視差を「分光視差」といいます。

　ここで恒星(銀河)までの距離の求め方、限界をまとめていきます。

　図－10

 

「βおうし」は実視等級1.7等、距離は 40PCである。左図を用いて、「βおうし」 の絶対等級を求めよ。 　 　また、分光視差、距離（光年）を有効数 字2桁で求めよ。

【解答】
　d=40PCであるので、上図より、M-m=-3、M-1.7=-3、∴M=-1.3　絶対等級は-1.3等

　d=1/p p=1/40=2.5×10^-2秒　d=40×3.26=130.4光年　

　分光視差　2.5×10^-2秒、
　距離　1.3×10²光年

 

 

　

　プロキオン（こいぬ座）はA、B二つの星からなる連星で、実視等級はA星は+0.4等、B星は+10.8等、スペクトル型はどちらもFである。

　また、プロキオンは図に示されるように、赤道座標による位置はおよそ赤経7h、赤緯+10°である。図中に示される曲線は黄道で夏至点（赤経6h、赤緯+23.4°)である。はある。以下の問に答えよ。

Q1　プロキオン（こいぬ座）は何月頃真夜中に南中するか、説明して答えよ。

Q2　プロキオンA、B２星はHR図上での分類はどのようになるか。

 

 

【解答】

　さあみんなで考えよう！宿題っ。

 

　「恒星の直径を見込む角」を「視直径」と言います。

　図－11

　太陽や月は「まあるく」見えて、太陽の視直径は32～33′（0.53～0.55°）、月のそれは30～33′（0.50～0.55°）ときわめて大きい値です。

　しかし、星を見たとき月や太陽のように「まあるく」は見えず、「点」にしか見えません。ですから、恒星の直径はきわめて小さいことが予想されます。

　以下の図-12から分かるように、恒星(B)の視直径(A)と年周視差(p)が求められれば、恒星の半径(R)（直径）がAU（天文単位、km単位にでも）で得られることが分かります。

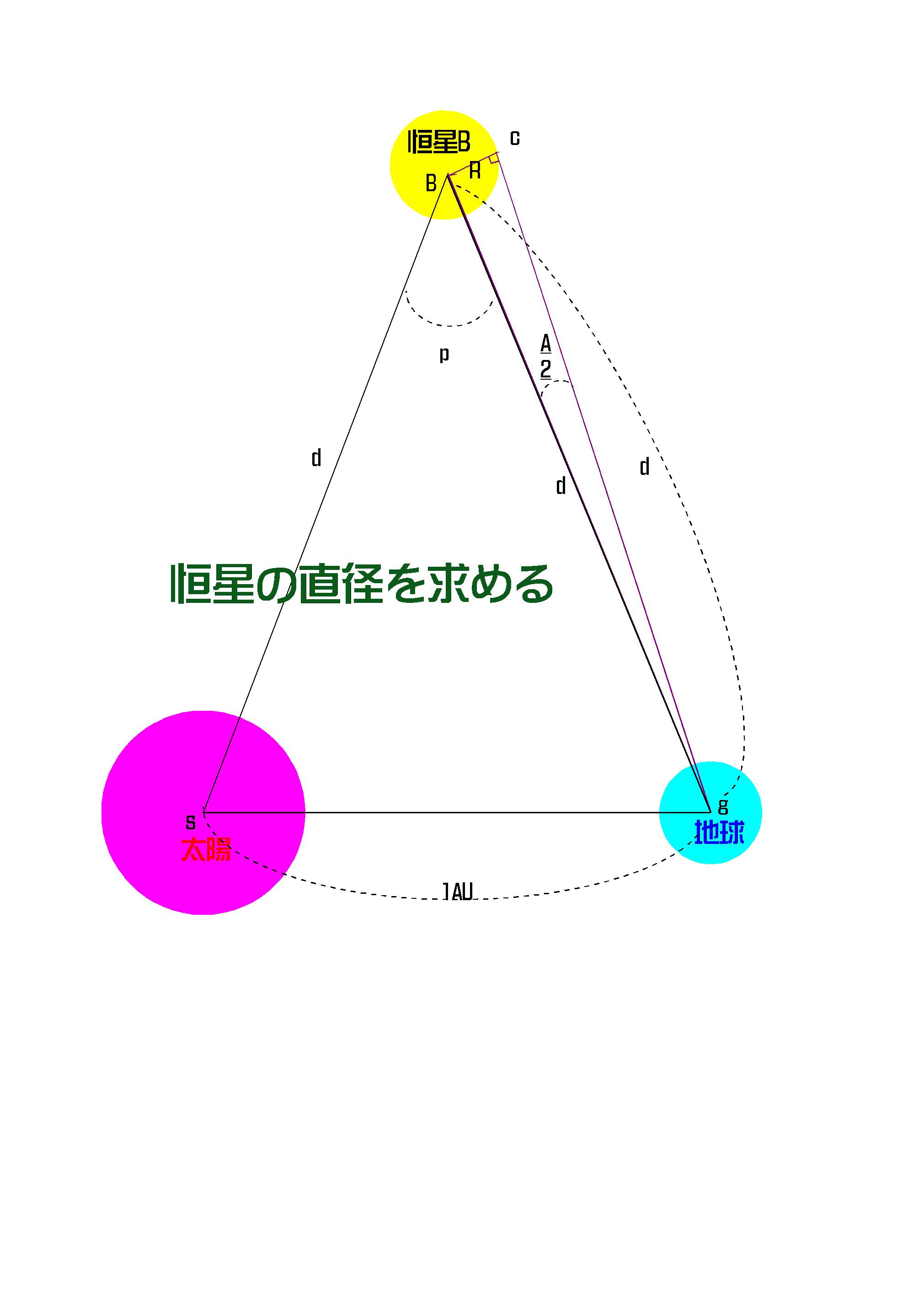
　図-12

　恒星Bがありその直径は2R、視直径はA(秒)、年周視差はP(秒)、距離はd(光年)であったとします。
　太陽～地球間の距離1AUは恒星Bまでの距離（d(光年)）に比べればはるかに小さいですから、距離gc＝距離gb＝距離sb＝d(光年)としてよいわけです。

　上の図-12は誇張されて描かれていますが、△bsg＝bを中心に半径dで描いた扇形bsgと見ることができますし、また△gbc＝gを中心に半径dで描いた扇形gbcと見ることができます。

　扇形の中心角に弧の長さは比例しますから、
p:1AU=A/2:R　R（AU）=A/2p　となって恒星の半径を求めることができます。

 

 

　

　恒星の質量は「連星」の場合に求めることができます。
　「連星」は二つの恒星がその共通重心周りに公転している天体で、質量が大きく明るい星を「主星」、質量が小さく暗い星を「伴星」といいます。

　（「主星」、「伴星」のことばは、なにやら、かつての人気漫画「巨人の星」の主人公、星飛雄馬（ほしひゅうま）、伴宙太（ばんちゅうた）に関係がありそうですが・・・。
　また物語の中で、星飛雄馬の父星一徹が「巨人の星となれ」と指し示した星が出てきました。この星は何か？、「巨人の星」を全巻読んで星家の家の見取り図まで書き出し、季節を考察して考えた方がいらっしゃいます。が、その話はまた後で。）　

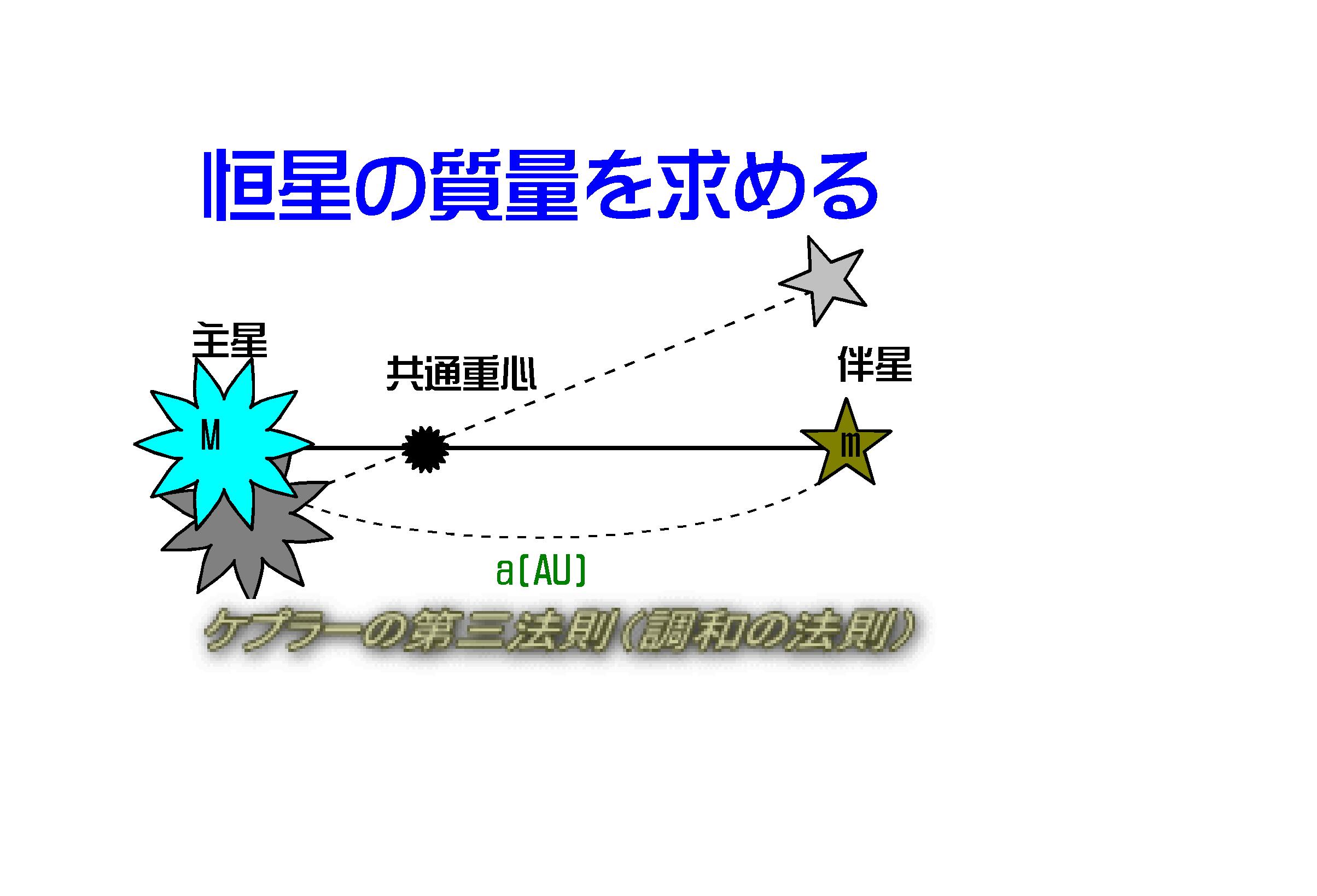
　図-13

　連星はケプラーの第三法則を満足して公転しています。T:公転周期（年）、a:平均距離(AU)、M、m:主星の質量・伴星の質量（太陽質量）、G:万有引力定数とすると、

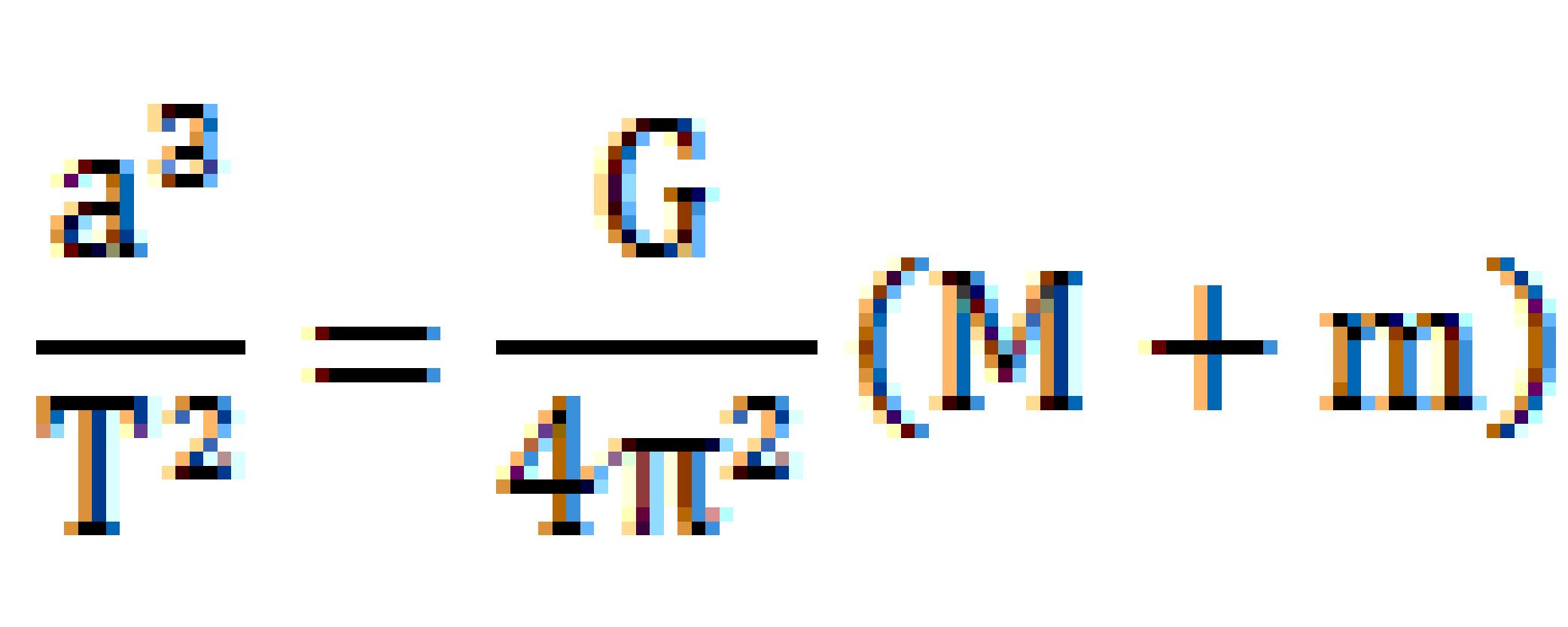
　が成り立ちます。∴

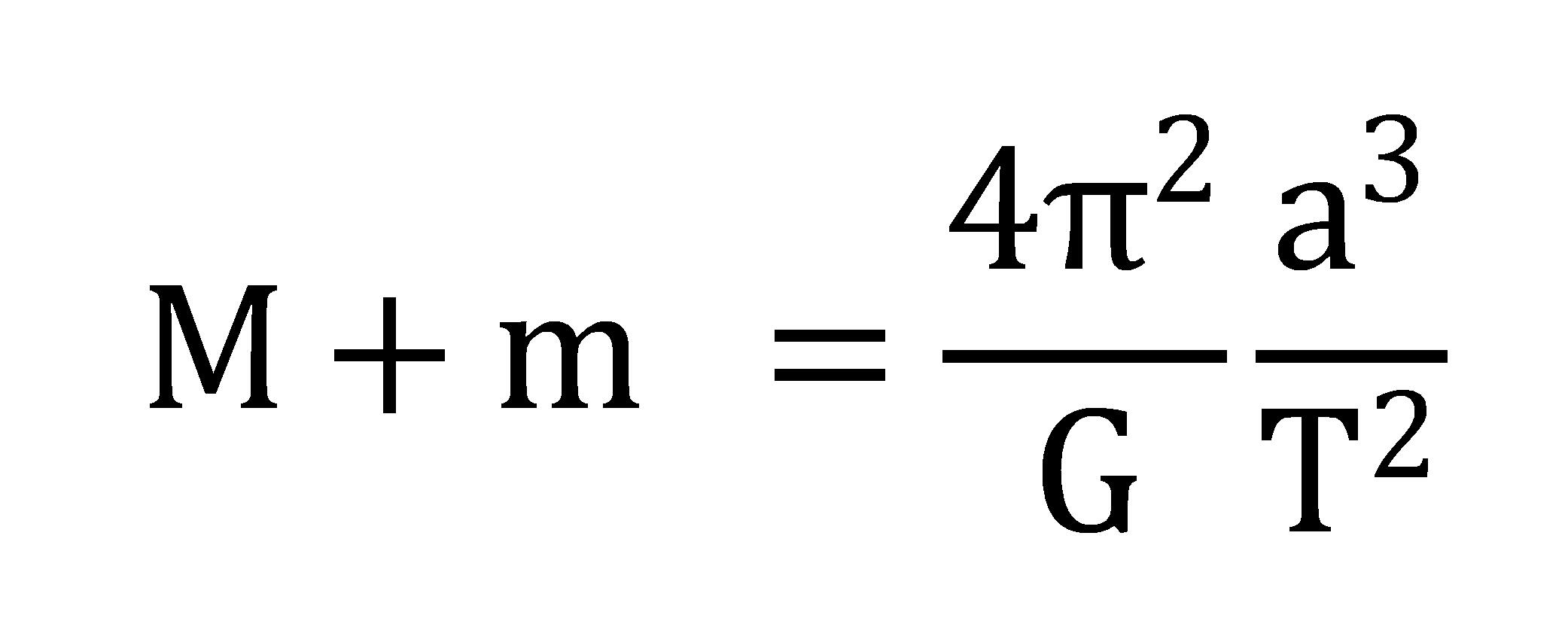
　・・これを①式、また「シーソーの公式」から

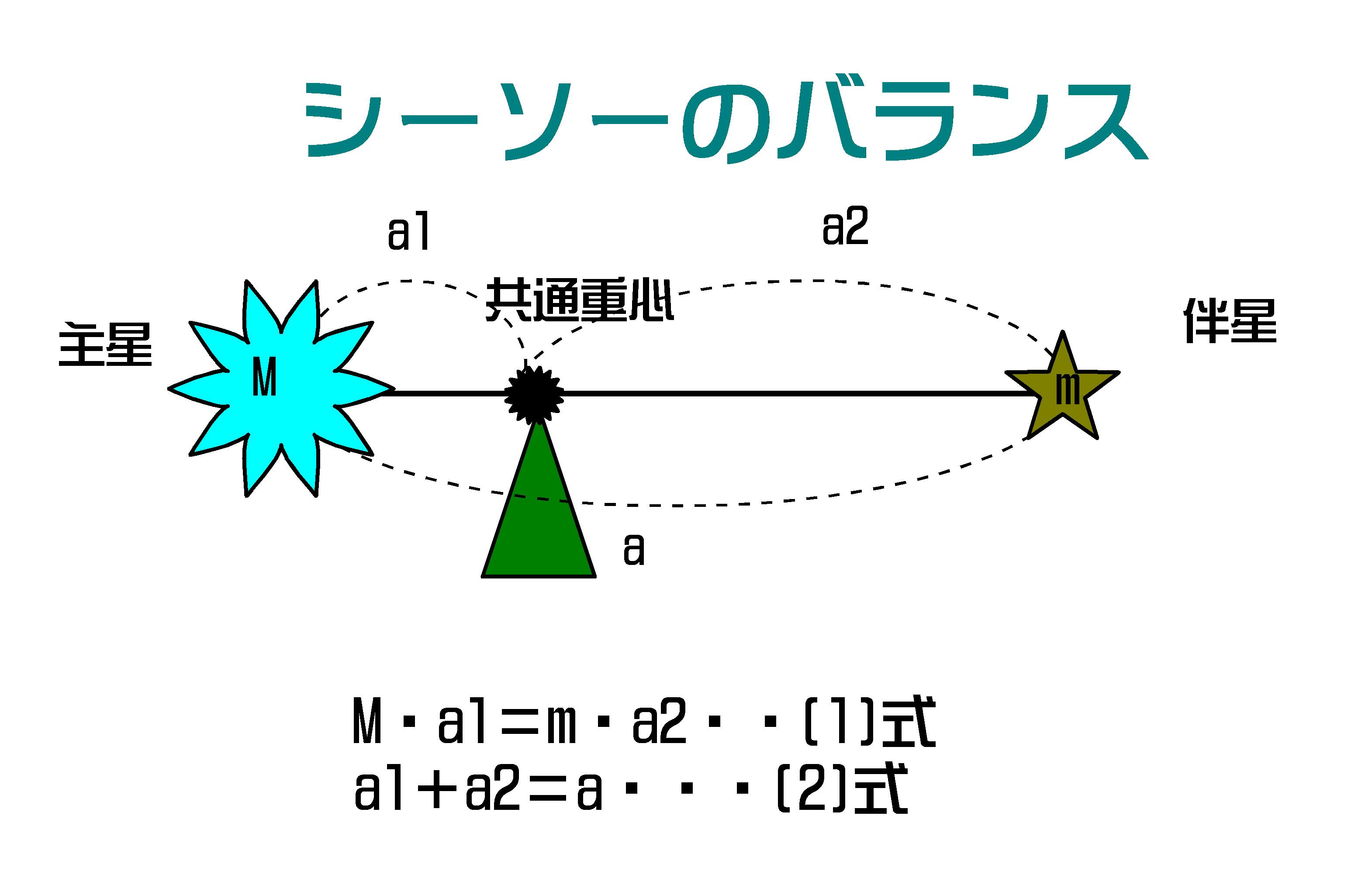
　図-14

(1)式、(2)式をあわせて②式

　ここでa1＝a－a2　(1)式のa1に代入してM・(a－a2)＝m・a2、　Ma－Ma2＝ma2　
　Ma＝Ma2＋ma2＝a2(M＋m）、∴

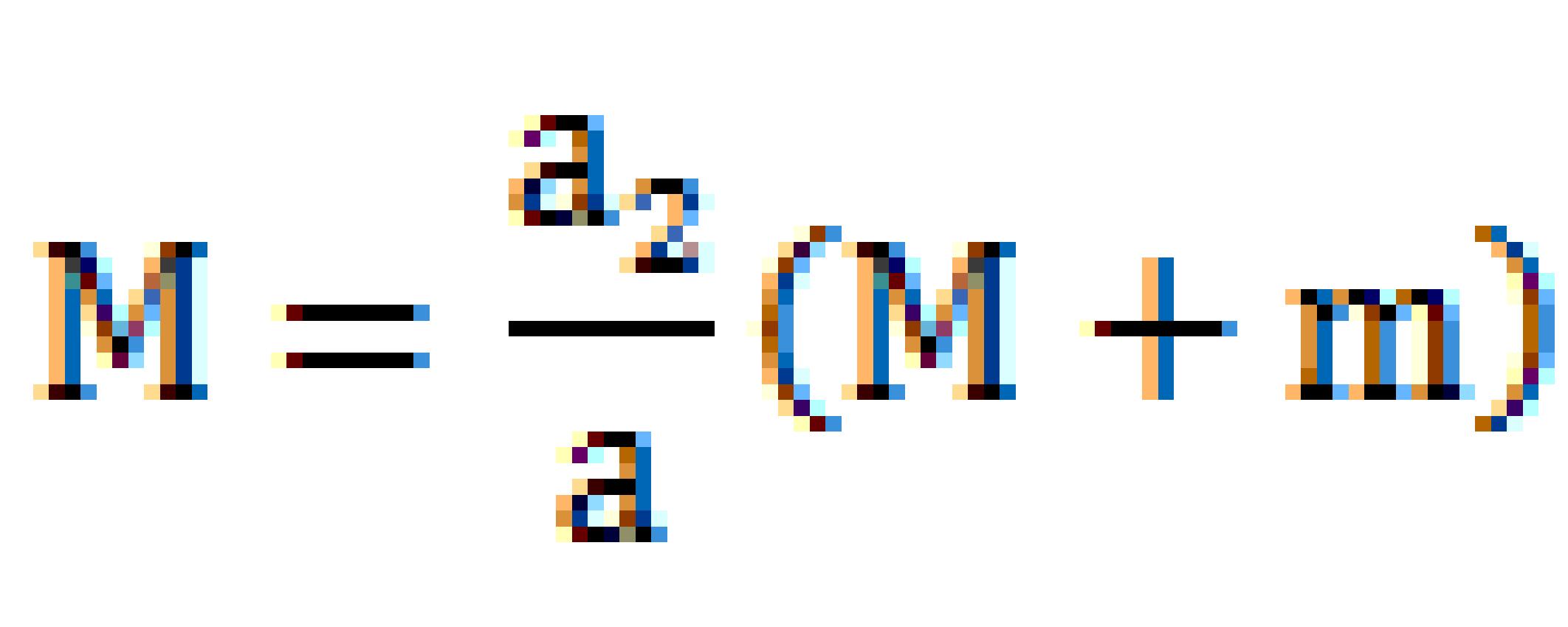
　ところで①式より

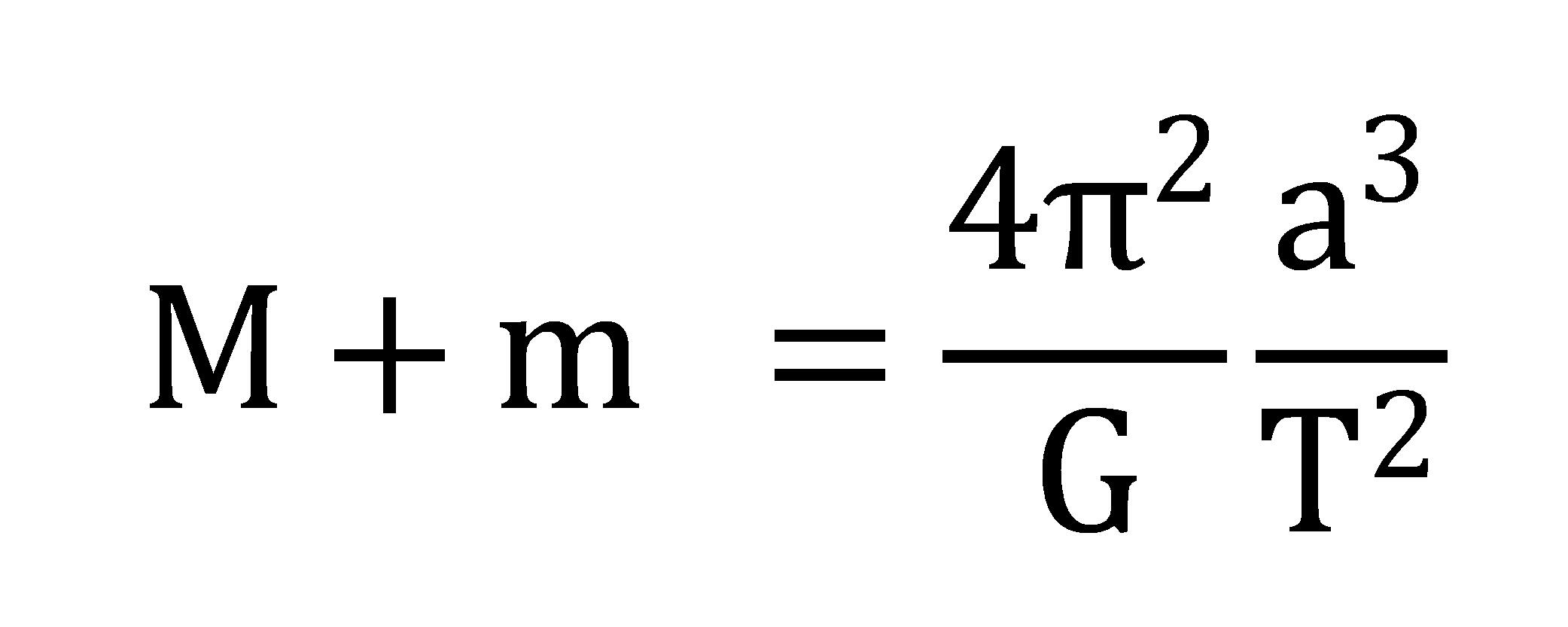
　ですから

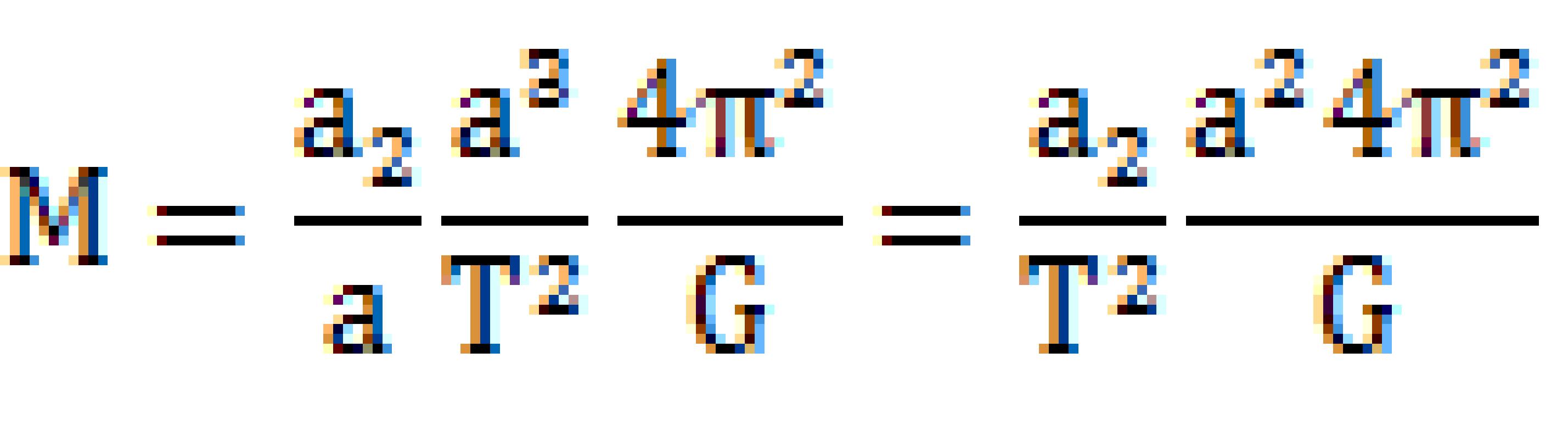
単位は太陽質量、同様に

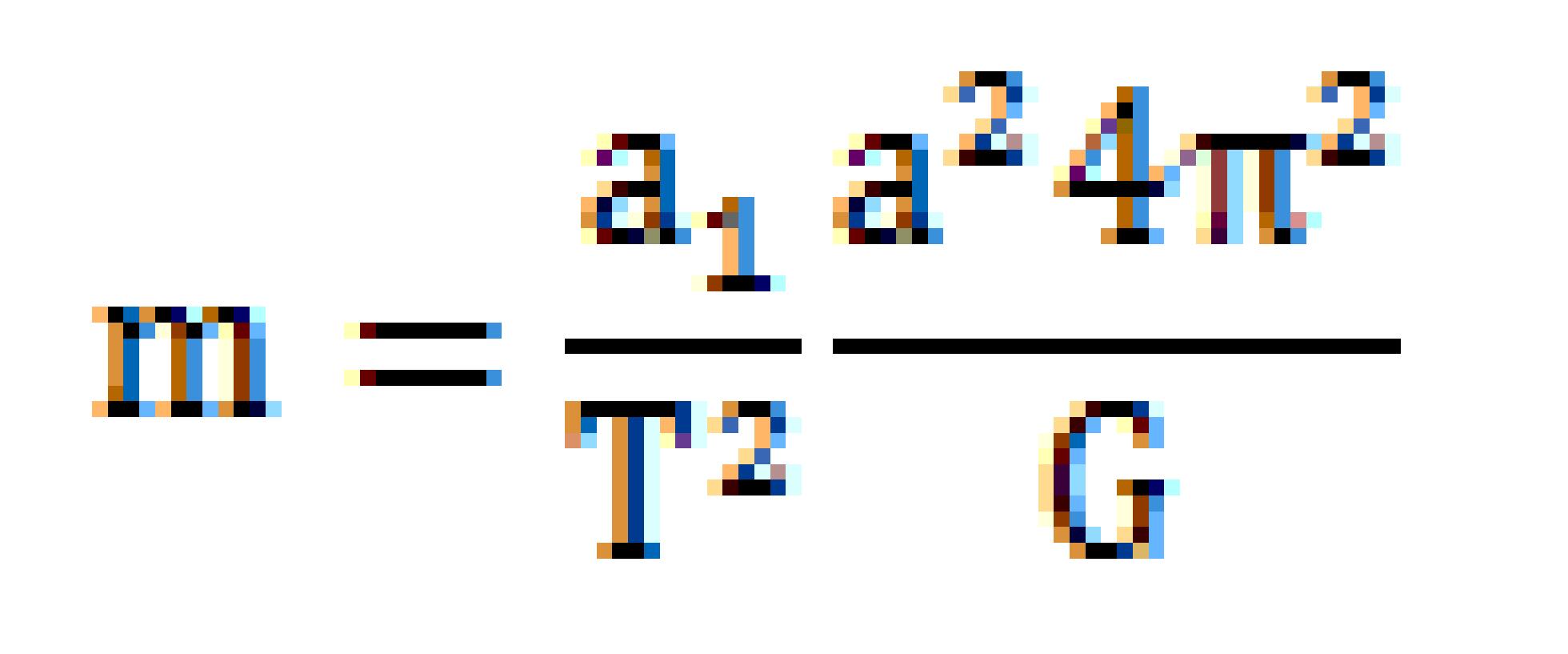
　となって主星・伴星の平均距離(a(AU))、公転周期(年)、共通重心の位置をそれぞれ観測によって知ることができれば、主星・伴星の質量が太陽の何倍かが求められることになります。

 

 

 

　連星はその共通重心周りに公転していますが、観測者の視線方向と連星の公転面とのなす角度によっては主星・伴星が互いに隠しあうことから、観測者は光度が変化するように見える場合があります。

　主星・伴星の公転周期は一定ですから、互に隠したり隠されたりする結果としての変光周期も一定になり、このような連星を「食変光星」といいます。図-15の場合は、観測者の視線方向と連星の公転面とが高角度で交わってますから、主星・伴星は互いに隠しあうことはなく食変光星とはなりませんね。

　図-15

　ところが視線方向と公転面と平行に近くなると、公転運動に伴って主星・伴星二つが見えたり、主星が伴星を隠したり、伴星が主星を隠したりして、それに伴って連星の明るさ（光度）が周期的に変化することになります。
　図-16では理解のため星の形を円形に表しています。

　図-16

　視線方向と公転面が一致していて、仮に主星の光度が3､伴星の光度が1。主星・伴星の断面積は2:1、そして公転運動によって主星・伴星が観測者に近づいたり遠ざかったりしても星の明るさには変化がないことにしましょう（図－17）。そして連星の公転運動の時間経過とともに、連星の明るさの変化をアバウトにグラフ化してみましょう。
　（連星は共通重心周りに主星も公転します。が、理解のために主星は真ん中に、伴星はその周りをまわるように図示しました。）

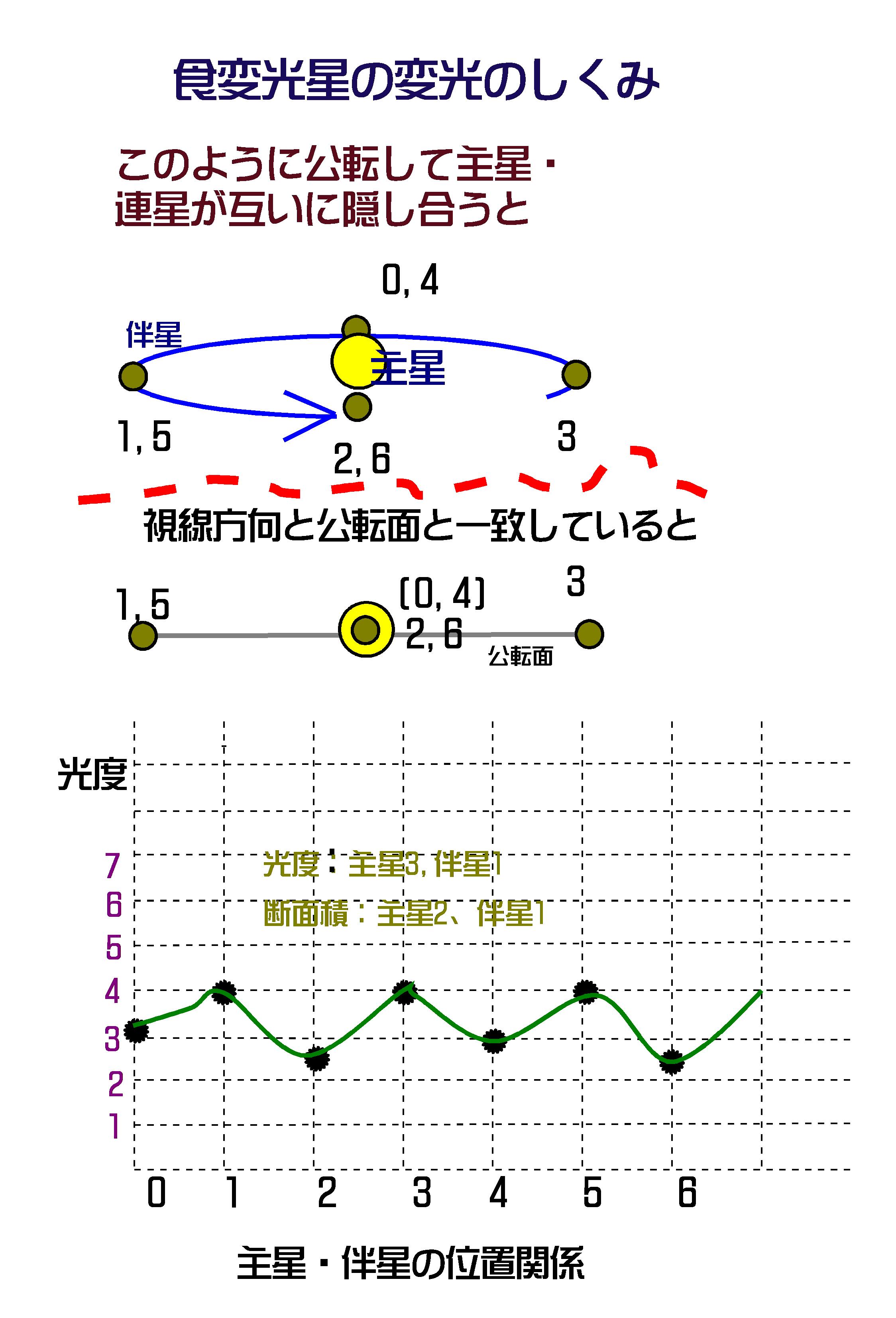
　図－17

（上の「光度変化と主星・伴星の位置関係の曲線グラフ」はお絵かきソフトの関係で、適切ではない表現になっています。詳しくは教科書・参考書を参照してください。）

　では、「主星と伴星の位置関係」と連星の「光度の変化（観測者から見た連星の光度変化）」の説明をします。

主星と伴星 の位置関係	連星の光度
0	伴星は主星の後ろに完全に隠れ、主星だけの明るさだけ→光度＝3
１	伴星が現れると、主星と伴星の両方の明るさを観測するので→光度＝4　この明るさは伴星が主星の前面（位置2）に入りきるまで続きます。
2	伴星が主星の前面に入ることにより、主星の半分が覆われ光度1.5。伴星の明るさは1ですからあわせて光度＝2.5
3	伴星が主星を覆うのをやめますから、再び主星、伴星の明るさを観測することになります。→ 光度＝4 この明るさは伴星が主星の後面（位置4）に入りきるまで続きます。
4	伴星が主星の後面に入ることにより、主星の明るさだけ→光度＝3
5	位置1 と同じ状態で、主星と伴星の両方の明るさを観測するので→光度＝4　この明るさは伴星が主星の前面（位置6）に入りきるまで続きます。
6	位置2 と同じ状態で、伴星が主星の前面に入ることにより、光度＝2.5

　図－18

 

 

　恒星のほぼ半分は連星であるので、上述のケプラー第三法則から主星・伴星の質量を太陽質量（「太陽の質量の何倍か」の単位（M◎で表す。））で求めることができます。
　では質量と光度（絶対等級）は、どのような関係になるのでしょうか。図－18の縦軸は絶対等級（上に向かって等級が小さい（明るい））、横軸は太陽質量にとってあります。
　一見して「重い恒星ほど明るい」ことがわかります。質量が大きいほど恒星の中心圧力が高まり、そのため温度が上昇し核融合反応が進み明るく輝き絶対等級が小さくなると考えられます。
　「重い恒星ほど明るい」関係を式に表すとおおよそ次のような関係（質量光度関係）になります。

 

　

　図－19

　質量光度関係（出典　宇宙物理学　共立出版　桜井邦朋氏による(2006)）　一部改変

　L∝M^22/5・Ts^4/5 L:光度、M:太陽質量、Ts：太陽表面温度で1924年イギリスのエディントンによって発表されました。
　高校地学では質量光度関係をL∝M³ないしはL∝M⁴ 、中をとってL∝M^3.5 として説明している場合が多いようです。

　L∝M^3.5−（1）式

　ところで「恒星の寿命（t）」＝「主系列星として輝いていられる時間」は次のように考えられます。
　「恒星の寿命（t）」は、「恒星の質量（M）」に比例し「光度（L）」に反比例する−。主系列星は水素の核融合で輝いていますから「燃料」が多いほど（Mが大）主系列星として輝きます。つまり、質量Mに比例します。

　ところが、明るく輝けば、輝くほど（Lが大）「燃料」を消費しますから主系列星としての時代を早く終えることになります。つまり恒星としての寿命は光度Lに反比例することになります。

　t∝M/L−（2）式　となります。

　ここで（2）式のLに質量光度関係のL∝M^3.5 を代入するとt∝M^-2.5となります。

　つまり、重い星ほど主系列星としての時間が短いことがわかります。逆に言えることは、HR図のO型、B型のような高温で明るい星が現在観測され（てい）ることは、宇宙の時代としては比較的最近生まれたばかりの恒星だと言えるでしょう。

　では計算で確かめて見ましょう。

　太陽の年齢は4.6×10⁹年（46億年）とします。太陽の質量をM◉、太陽の寿命をt◉とします。
　t∝M^-2.5 ですからt◉∝M◉＝4.6×10⁹年

　上の図から、絶対等級M=－5等の主系列星の質量は、太陽の10倍と読めます。この星の寿命をt-5等とすると、
　t-5等∝(10M◉)^-2.5 =10^-2.510M◉=4.6×10⁹×10^-2.5 =4.6×10^6.5=4.6×3.16×10⁶=1.45×10⁷年　およそ1500万年前＝新生代新第三紀中新世に誕生した星ということになります。

　一方、絶対等級M=＋10等と暗い星はどうでしょう？

寿命をt+10等とすると、
t+10等∝(10^-1M◉)^-2.5 =10^2.510M◉=4.6×10⁹×10^2.5=4.6×10^0.5×10¹¹=4.6×3.16×10¹¹=1.45×10¹²年　計算上では一兆年と出てしまいました。

　「大盤振る舞いはいけない。巨星落ちやすし。　貧しくも慎ましく、細々と暮らすのがよい」－そういうことでしょうか。

 

 

 

　ケフェウス変光星（ケフェイド　または　セフェイド　Cepheid）と周期光度関係
　小マゼラン雲（当時、地球からの距離は技術的に測定できなかったので距離不明）に含まれる25個（約100個という説もあり）の変光星を研究し、変光周期と光度の比例関係を発見した（1908年）のはヘンリエッタ・スワン・リービット(1868～1921、米国)で，1912年に周期光度関係を発表しました。

　図－２０　リービット肖像
　西條敏美(2011)地球から宇宙へ、
　恒星社厚生閣より引用（一部改変）

　この変光星は変光周期が長い星ほど絶対等級が小さい（明るい）という性質があり、これを周期光度関係と呼んでいます。周期が 1日以下のものをこと座RR型変光星とよんでいます。

　小マゼラン雲は地球からきわめて遠方にあり、一方では25個の変光星は小マゼラン雲という小さなエリアの中に含まれると仮定しますと、地球から25個の変光星までの距離はおおむね等距離としてもよいことになります。縦軸に光度、横軸に変光周期（対数目盛）をとってグラフ化したところ明瞭な比例関係が見いだされたわけです。

 

図－２1（出典　野本憲一・定金晃三・佐藤勝彦（編）MA7シリーズ現代の天文学　日本評論社　2009）

図－２2

 

　
　25個の変光星の光度（平均）は見かけの明るさ（実視等級m）ですが、等距離にある（と考えて扱うことにした）のですから32.6光年（10PC）の距離に持ってきたとしても、25個の変光星の光度（差）には変化は生じないはずです。したがって、正確ではないにしろ25個の変光星の見かけの光度（実視等級m）を絶対等級（M）の扱いとしてもかまわないことになります。ただ、等級をいくら減じて絶対等級を求めるかが問題です。

　その一つの方法は次によるものがあります。ケフェイドと主系列星からなる連星を探索します。この際ケフェイドと主系列星の太陽（地球）からの距離は同一とみなします。以前学習した「恒星の質量を求める」から、主星・伴星の平均距離(a(AU))、公転周期(年)、共通重心の位置をそれぞれ観測によって知ることができれば、主星・伴星の質量が太陽の何倍かが求められることになります。
　連星の主系列星の質量が太陽質量で求められますから、「質量光度関係」から主系列星の絶対等級(M)が推定されます。実視等級(m)は観測によって得られますからM-m=5-5log ₁₀d より主系列星の距離＝ケフェイドと主系列星からなる連星の距離が求められる−というものです。

　リービットが周期光度関係を発表した翌年の1913年、 HR図（ヘルツシュプルング・ラッセル図）のヘルツシュプルングは周期光度関係を用いて小マゼラン雲までの距離を3.0×10⁴光年と計算しました。また1923年ハッブルはアンドロメダ銀河に含まれるケフェイドについて同様な計算を行い9×10⁵光年と発表しました。その当時、我々の銀河の大きさは3×10⁵光年と考えられていましたから、銀河をずーっと超えてしまった遠くにある系外銀河ということになってしまったわけです。
　現在では小マゼラン雲までの距離＝約1.98×10⁵光年、アンドロメダ銀河までの距離＝約2.60×10⁶光年と訂正されています。

telescope、tube、magnitude、、confirmation、、concept、、radiation、、sence、logarithm、（common logarithm）、　formula、constant、、inverse proportion、、surface、systamatically、absorb ,(n)absorption,(a)absorptive、center gravitaion、（nuclear 　division,）　nuclear fusion、（milky way , ）galaxy