海のスライドショー
1 宗谷岬
北海道稚内市にある日本国内最北端(北緯45.5度)の岬(写真は8月27日)。1976年、音楽グループ「ダ・カーポ」が「宗谷岬」を歌って有名になりました
2 襟裳岬
日高山脈は北海道の南北の脊梁となっており、北部の日高ポロシリ岳が最高峰。おおむね南下するにしたがい高度を下げて襟裳岬で太平洋に没します。
風が強く吹くところで、樹木がなく笹がわずかに生い茂っています
3 川平湾(かびらわん)
沖縄県石垣島(写真は11月22日)。西表石垣(いりおもていしがき)国立公園(北緯24度)として指定されています。船底が透明になっていて(グラスボート)、海底の様子を観察出来ます
4 佐渡島・尖閣湾
佐渡弥彦米山国定公園に属する長さおよそ50kmの海蝕崖に位置します。写真のように、日本海の激しい荒波が断崖絶壁を作り出しています
5 エーゲ海
(サラコニス湾:写真は12月22日)
アテネの南西約30kmのエギナ島に向かっています。 エーゲ海には石灰岩・大理石からなる約2500の島嶼があり、エギナ島は最大の島です。ピスタチオナッツがシリアから持ち込まれ、現在では有名な農産物となっています
6 アドリア海
ドブロブニク・クロアチア イタリア半島の北東に何千kmも続くカルスト地形が広がりそこに挟まれたアドリア海。海の青さ・赤い屋根の瓦・白壁の美しい街です。その美しい光景の裏には、1990年代の内戦があり多くの命が失われたことを忘れてはなりません
タイトルの「海洋」-英単語を思い浮かべれば、sea、oceanが出て来るでしょう。sea、oceanの違いが一体どこにあるのだろう?
日本海=Sea of Japan、東シナ海=East China Seaなどなどであるのに対し、太平洋=Pacific Ocean、大西洋=Atlantic
Ocean、インド洋=Indian Oceanなど、oceanが「付く」海は「五大洋」ですね。
このことから、ここで何となく「sea」は規模が小さく、「ocean」は大きいらしい事に気がつきます。
人間・地球にとっては「sea」でも「ocean」でも生命の誕生となった場という意味合いでは重要であり、充分大きいことには変わりません。
南の石垣島(北緯24度)から北の宗谷岬(北緯45.5度)まで、距離は約2000km以上離れています。
ご覧のとおり海の色は場所、天気により全く異なります。石垣島のように南の海の場合、有機物が少ないためプランクトンが少なく「青」色が強調されます。さらに、浅い海のため海底の「白」と混合されエメラルドグリーンに見えます。
一方、北の海は窒素・リンなど有機物が多いためプランクトンが多く含まれ透明度が低くくなります。
クロアチア(ドブロブニク)・アドリア海(写真は7月4日) 図-1
海の色(+空の色)の青さの説明にはこれでは不十分です。太陽光は虹や、プリズムの屈折によって知られるように、人間が知覚できる色としては「長波長←赤・橙(オレンジ)・黃・緑・青・藍・紫→短波長」の7色です。
太陽から発せられるこの7色は強さは等しくありません(下図参照)。図は、物体(太陽)の表面温度が6000度(K)、その表面からは紫外線、visible=可視光線、赤外線、電波が放射されることを示しています。少し見にくいですが、表面温度が6000度(K)の場合、藍・青色が強く、黃・橙(オレンジ)・赤の順に弱く放射されていることが分かります。
波長の長い赤・橙の色は大気中の気体分子、海水の水をはばかることなく直進します(電磁波としての波長が長いため)。
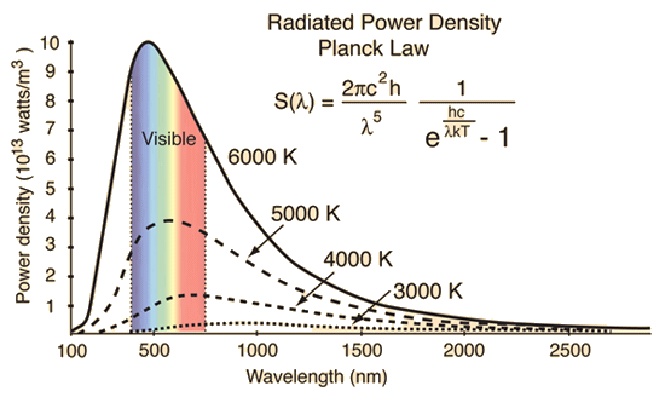
山賀 進氏のWeb siteより借用 図-2(縦軸が強度、横軸が波長 波長に対応した色が示されています)
一方、比較的短い波長の緑・青・藍・紫は分子に衝突して散乱させられます。つまり、海で言えば赤・橙色は海底に向かって行ったきりになるのに対して、緑・青・藍・紫色は乱反射して戻って来て、その合成した色をわれわれは「海の色」として見ることになるわけです。
地球表面の29.2%は陸地で、その平均の高さはおよそ840m、地球表面の70.8%は海洋でその平均の深さはおよそ3800mと言われています。
平均の高さ840mの陸地の地層・岩石を海洋に入れ、埋め立てようとすると足りず、深さ2440mの地球ならぬ「水球」になってしまうんです。
地球は46億年前に誕生したとされていて、海洋が形成され現在の海水の組成と等しくなったのが20億年前と言われています。それほどに気の遠くなるほどの時間が経過しており、それゆえ「海洋」=海は泰然自若とした存在です。

海水の濃度(塩類の濃度)は、百分率=%ではなく、千分率=パーミル=‰で表します
| 薄い海水 | 33g/1000g=33‰ | 河川水などの流入で薄められるから |
| 濃い海水 | 38g/1000g=38‰ | 水分の蒸発(EX.亜熱帯高圧帯)で煮詰められるから |
平均の濃度=35‰


塩素濃度を測定して海水濃度を求める方法
S=1.81・x+0.03、S=海水の濃度、x=塩素濃度、

海水の電気伝導度の測定して海水濃度を求める方法

海水には食塩(塩化ナトリウム=NaCl)だけ解けているわけではありません。地球創成時に長期間降り続けた雨と火成岩と反応し、様々な塩類(+大気には様々な気体が含まれており、一部は海水に溶解している。)が海洋にもたらされています。(EX.硫酸ナトリウム)
塩類の多い順に
NaCl、MgCl2(塩化マグネシウム)、Na2SO4(硫酸ナトリウム)、CaCl2(塩化カルシウム)
これの覚え方はNa(な)、Mg(まぐ)、Na(ない)、Ca(か?)=「生臭くないか?」
このほかイオンとして、HCO3-(炭酸水素イオン)、F-(フッ化物イオン)、Br-(臭化物イオン)、K+(カリウムイオン)ほか含まれています。
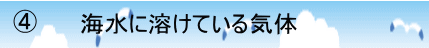

酸素、

二酸化炭素
海水は大気の二酸化炭素量の調節を行う=海生植物の光合成、海水自身の吸収

図-3
図-3は、海洋の水温と水深の関係をシェマティックに示したものです。
「黄」曲線は夏季、「白」曲線は冬季を表しています。
「お絵かきソフト」の関係から、曲線の「曲がり方」が教科書のようではないことに注意して下さい。例えば、冬季の季節的水温躍層の部分が比較的に「等温」に表現されています。
☆ 季節的水温躍層:
夏季には日光のエネルギーを得て海面の水温は上昇し、冬季には冷却されます。「水温」が「躍動的」に変化します。
夏季は海面付近は約28℃、冬季は18℃。
☆ 表面混合層:
海面上を吹く風、波によって攪拌・混合され、深さ500m程度まで水温が比較的に等温。冬季は冷却された海水が沈降し、表面混合層の厚さは増します。
☆ 主水温躍層:
「主」は「年間をとおして」の意。「主人」、「主婦」の言葉がありますね。いつも家にいる人、婦人-そういう意味です。500m~1000mの深さにあり、水温・塩分濃度が急変します。主水温躍層が高緯度の海面に現れたところを「極前線」といいます。
☆ 深層水層:
地球の両極付近で冷却された表層水が沈降し、深層水となります。上層から、中層水、深層水、底層水に区分されゆっくりと移動しています。
世界の深層水の起源と循環
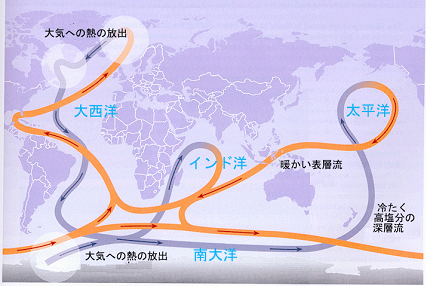
(出典:気象庁:「深層循環の変動について」 図1) 深層循環の模式図)
世界を広く循環する深層水の起源は上の図の「大気への熱の放出」と記された所で、暖かい表層流が冷却されその結果密度が大きくなって沈降し深層水となっています。その場所は、南は南極大陸ウエッデル海付近と、北はグリーンランド海付近の2か所のみで、深層水の緩やかな循環は同時にエネルギーの世界的な規模の循環も果たしています。


海流とは:「同じようなところを、同じような方向に向かう、比較的に強い海水の流れ」をいいます。
☆ 吹送流:
偏西風、貿易風などによって海水が吹き寄せられてできる流れで、海流の主な原因。
☆ 密度流:
海水の水温、塩分濃度の違いから、海水に密度の違い「重い」・「軽い」が生じ、そのために生じる海流。
☆ 傾斜流:
海面に高低差が生じた結果、 そのために生じる海流。
☆ 補流:
海水が移動してしまったあと、その部分を補う流れ。

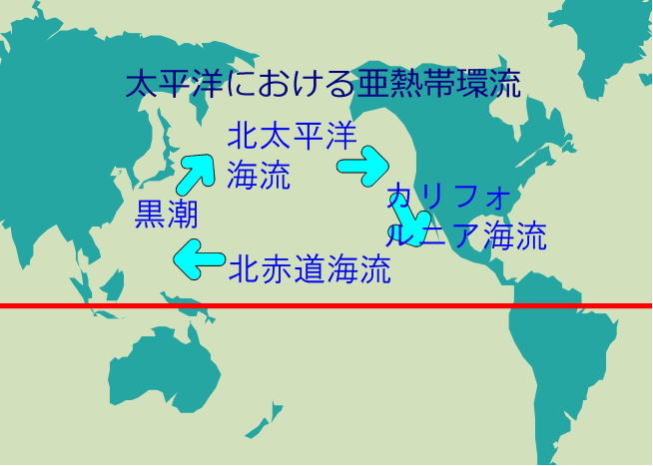
図-4
地球を取り巻く大洋に北半球においては時計回り(右回り)の、南半球においては反時計回りの環流が見られます。
これは、海面を吹く偏西風・貿易風、地球自転が原因となる転向力によるものです。
「西岸強化(流)」
図-4の四つの流れのうち、黒潮の流れが強い。大西洋でも、南半球でも「大陸の西の岸に強い環流」が見られ、「西岸強化(流)」と呼ばれています。

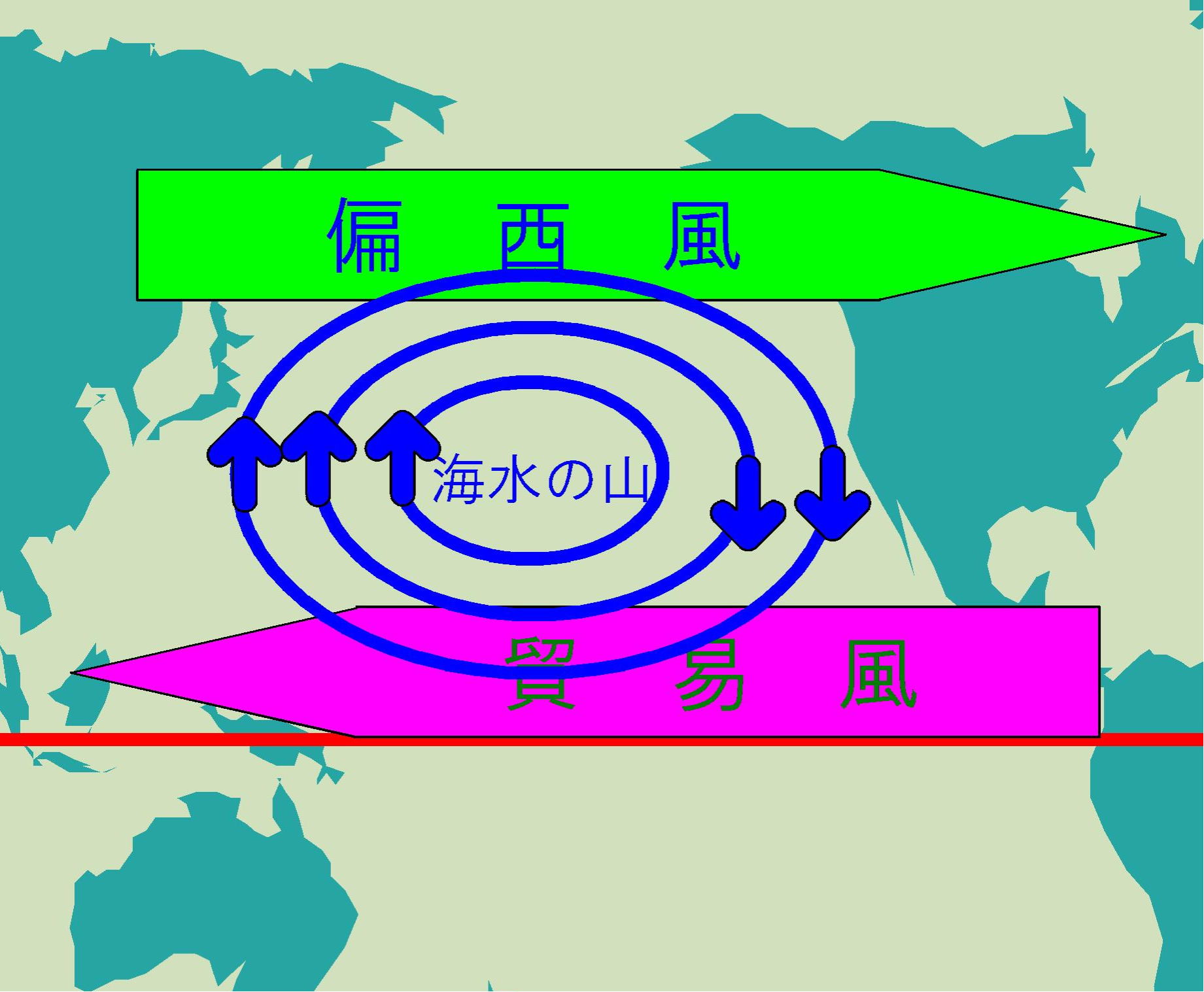
図-5
赤道付近には貿易風が、中緯度付近には偏西風(図-5は、かなり高緯度の位置に表現されています。)が吹いています。
転向力の効果が緯度によらず等しければ、直角右向きに海水は運ばれ、太平洋の中央に海水の山ができることとなります。
地衡風と同じように「高圧部を右に見て等圧線と平行に吹く(流れる)」ので、時計回りの亜熱帯環流が形成されます。
しかし、これではどこでも流れの強さは等しいことになってしまいます。
ところで転向力:F、運動する物体の質量:m、流速(風速):v、地球自転の角速度:ω、緯度:θとすると、
F=2mvωsinθ
の関係がありました。
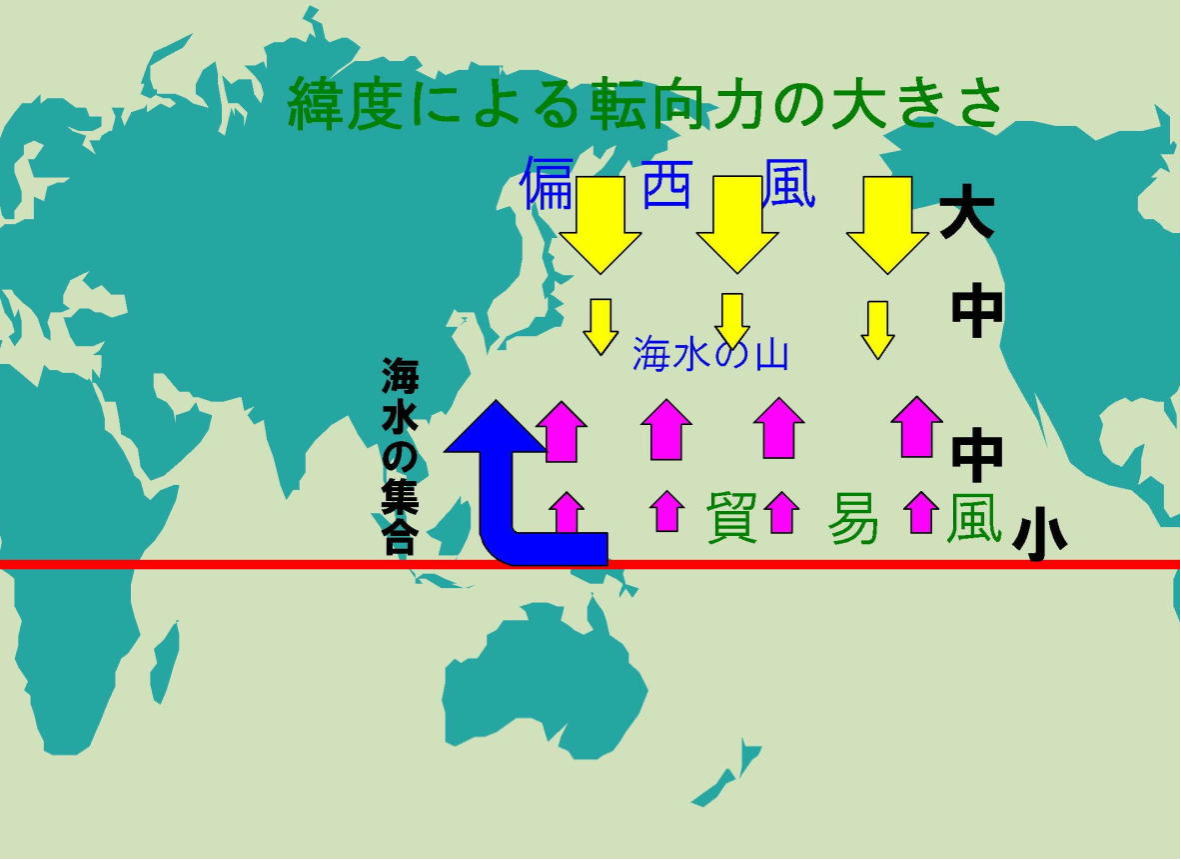
図-6
この式から、高緯度ほどsinθの値は大きくなると同時に転向力が大きくなり、流速vが増します。
その結果、偏西風の卓越する海面付近では南下する流れが(エクマン水送流)が加わります。
「南下する流れ」とは「北太平洋海流」としてアメリカを目指して向かったものが、「南下する流れ」を持ったために「カリフォルニア海流」(北緯40度付近)では弱くなっていることを意味しています。(図-6、偏西風域帯)
また、低緯度付近を東から西に定常的に吹く貿易風域帯においては、気圧傾度力が小さくそれに釣り合う転向力も小さくなります。その結果貿易風の風速も小さくなります。
しかし、北に向かって緯度θが大きくなるにつれ風速が大きくなるにつれ、流速(東→西)も大きくなります。(図-6、貿易風域)
大陸の東岸付近(低緯度~中緯度)においては、上述の「偏西風域帯からの南下流」と
「貿易風からの北上流」と拮抗するようになり、一見流れの無いような状態になります。(図-6、右)
太平洋の中央では、「偏西風域帯からの南下流」と「貿易風からの北上流」が集結し、「海水の山」を築くこととなります。ここでの海流の説明は図-5とほぼ同じで良いでしょう。(図-6、中央)
低緯度の貿易風帯では、海水に対して東から西向きに働きかけ、加速させ海流はパラオ・フィリピン島付近で北上を行います。(図-6、左)
一方、大陸の西岸(低緯度~中緯度)では、 パラオ・フィリピン島付近で北上した流れに「貿易風からの北上流」が加わり、流れが強化されます。(図-6、左)
これが大陸の東岸付近と大陸の西岸付近に流れる環流の強さの違いで、「西岸強化(流)」と言われる所以です。(図-7)
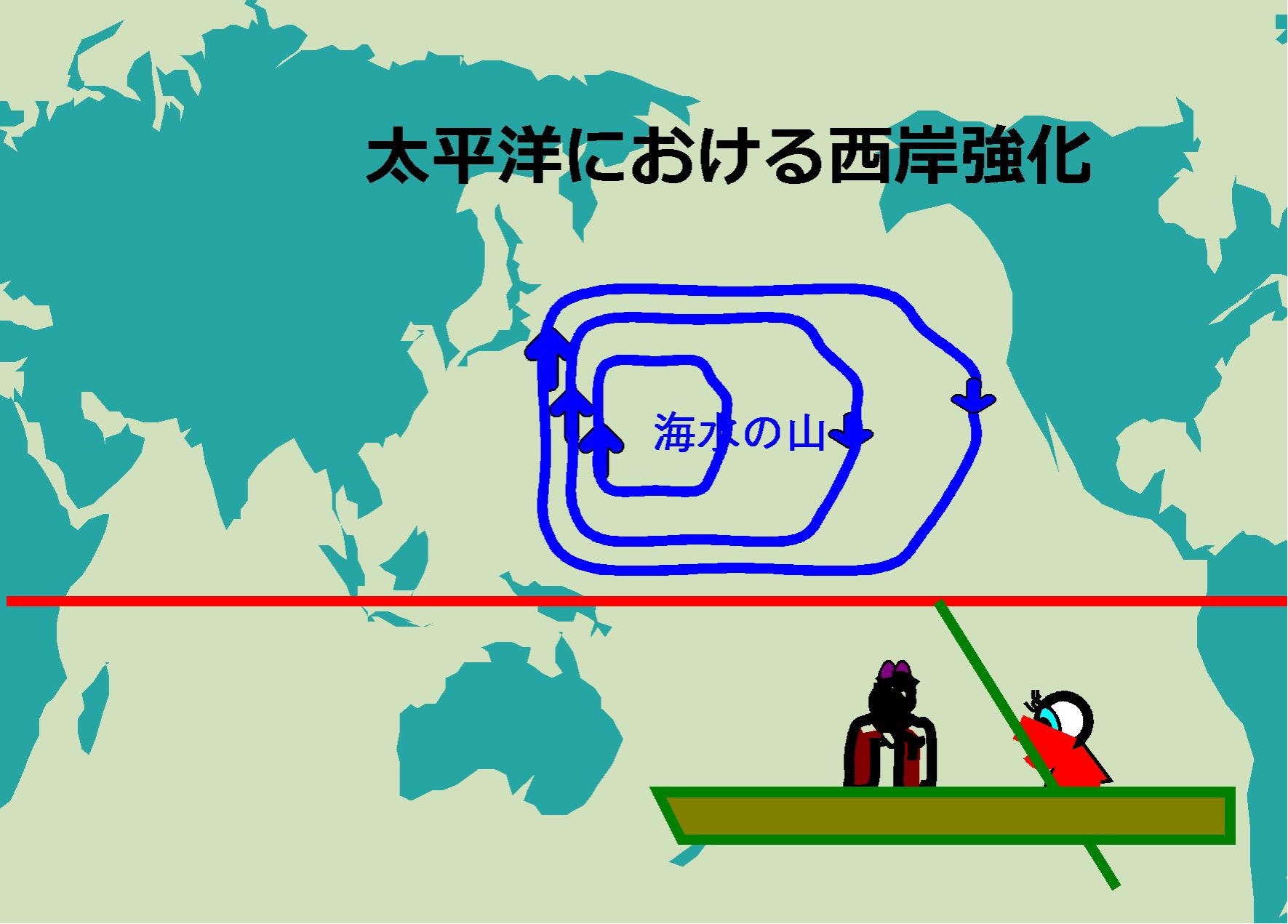
図-7


(おことわり:出典(原文)は加地伸行著「論語」角川文庫によります。原文では「筏」は別な文字になっております。)
上に掲げる文は、「論語」公冶長 篇七の一節である。
課題一 全文を書き下し文にし、和訳せよ。
課題二 傍線①について説明せよ。
課題三 傍線②由、子路について説明せよ。
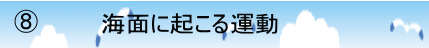
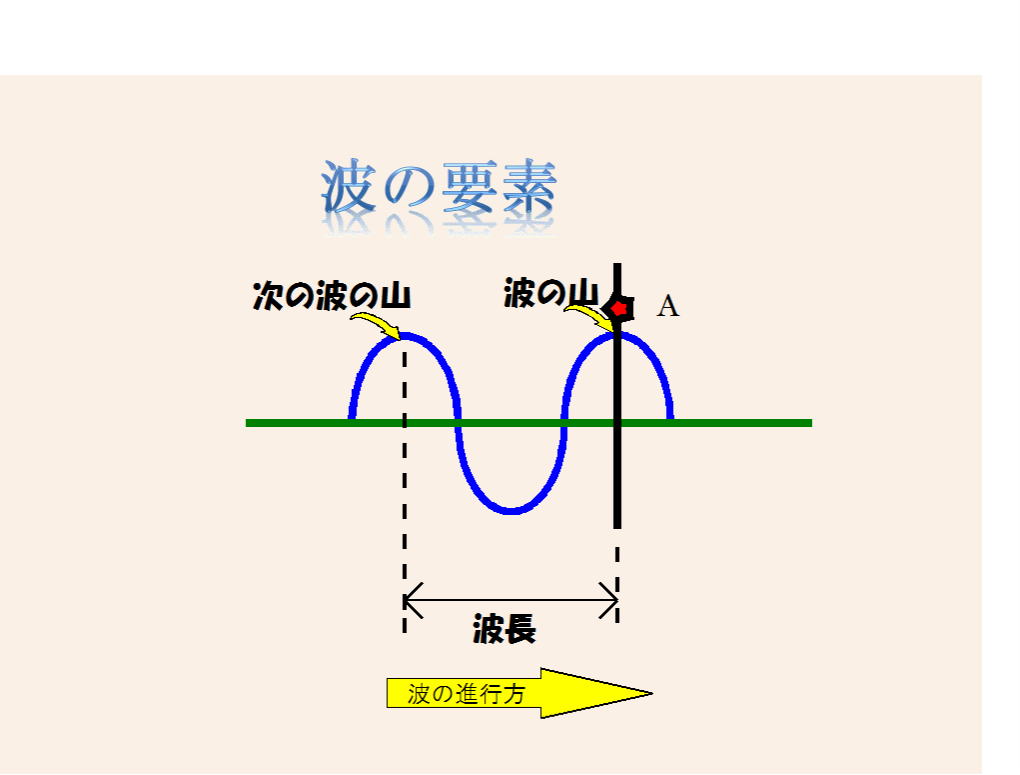
図-8☆ 波の要素
波長(L)=波の山から次の山までの長さ
周期(T)=波の山(谷)がある地点(図-8では、A)を通過してから、次の波の山(谷)が通過するまでの時間
波の伝わる速さ(V)=波の山(谷)がある地点(図-8では、A)を通過してから、次の波の山(谷)が通過する速さ。
波の伝わる速さ(V)=進んだ距離÷時間
=波長(L)÷周期(T)
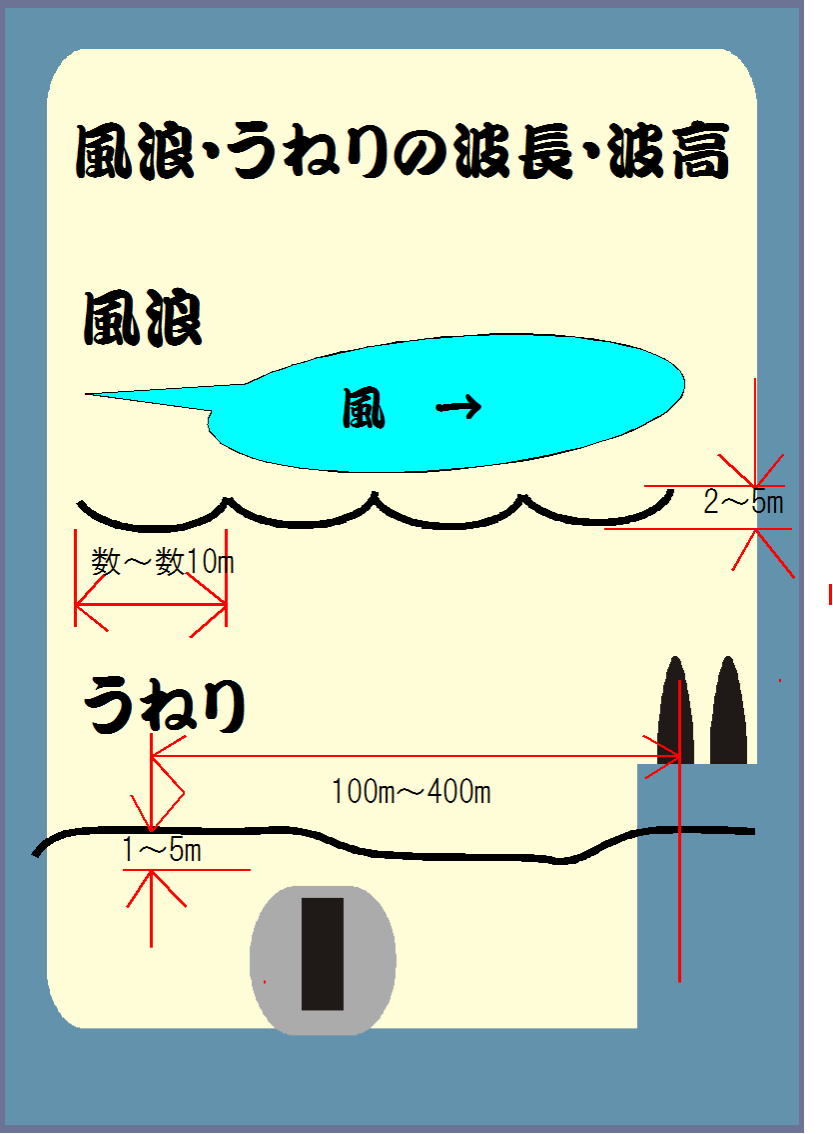
図-9
☆ 波の分類
①表面波=風浪、うねり
・水の分子が表面付近で円運動するためにできます
・波長が水深に比べて小さい
風浪=風の影響を直接受けている波
うねり=風浪が波の発生域を出て、風の直接の影響を受けなくなった海面の動揺
②長波=津波
・水の分子が楕円運動によってできる波で、海面から海底までの水が動揺しています。
・波長が水深よりはるかに大きい
風波は「ザブン」(勿論、相当のエネルギー、破壊力を持っている)であるのに対し、3.11.で身を以て経験したように「津波」は非常に恐ろしいものだということ-です。
「tenki.jp」にアクセスすれば日本はもとより、世界の天気、火山情報、地震情報を入手することができます。
地震について多くの人は、日本国内で1日にこんなに何回も地震が起きているなどとびっくりするのではないでしょうか。
津波が発生しないのは、地震の規模が小さかったり、震源の位置が海底近くでなかったり、「偶然」・「僥倖」なのかも知れない-のです。
ある音楽グループが今から十数年前に「津波」をタイトルに歌っていました。我が耳を疑いました。何人もの生命を奪ってきた「津波」を歌のタイトルに用いるとは・・。
「津波」をタイトルに作曲した発想・意図は、押したり、引いたりする波ように男女の想いが行き交う様を「津波」と表現しようとしたようです。
過酷な自然現象を表す言葉、「地震」の他、例えば「日照り」、「長雨」、「大吹雪」、「噴火」・・これらの言葉を用いて、仮に男女の恋心を歌詞や歌のタイトルに用いる-とします。過去にも現在においても被災し、心に大きな傷を受けた人が沢山いることは間違いなく、その方々の心情を察すれば、仮初めにも恋の歌を作るなど、発想は及ぶものではありません。

まず、津波の速度を求めてみましょう。波長Lを、L=100km(105m)~1000km(106m)、周期Tを、T=10分(600秒)としてみます。
速さ(V)=波長(L)÷周期(T)より、
V=166.6m/杪~1666m/杪
V=597km/h~5970km/h
と計算上は大きなスピードになりますが、沖では900km/h(国際線ジェット機の速度)、陸近くで250km/h(新幹線の速度)、渚では摩擦でスピードが遅くなり40km/h(秒速10m以上)ほどになります。
渚付近で津波は、時速40km、秒速10m以上で「非常に速い」と認識すべきです。陸上の選手が全力で10秒走ったとしても100mしか進まない。すぐに津波に追いつかれてしまいます。
あるとき「高さ1mの津波」の襲来が予想されたとします。(図-10)
図-10
その規模を簡単に次のように見積もります。
津波は長波なので、長さ100km(100000m)、高さ1m、幅2km(2000m)の水の立方体(体積=V)の移動と考え、その質量(密度1ton/1m3)を求めます。
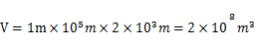
すなわち2✕108 トンの水塊となります。
ところで以下の写真のCAT b11Tブルドーザは幅5.6m、長さ10m、運転質量103トンとのことです。
簡単に言えば、2✕108トンの水塊は、200万台分のブルドーザに相当し、これが押し寄せてくることになります。

(おことわり。写真はCAT-japan.jpのHPより借用しました。)
チリで発生した津波が太平洋を越えて何時間で日本にやってくるのでしょう
津波の速さをVL(m/杪)、重力加速度をg(m/杪2)、津波の伝わる海の平均水深をh(m)とすると、
VL=√gh の関係があります。
太平洋の平均の水深を4000m、重力加速度g=10m/杪2とすると、津波の速さVLは秒速いくらになるか?
また、その津波が18000km離れたチリ沖で発生したしたとして、日本沿岸に到達するのに何時間かかるか「ためして計算!」してみましょう。
まず、津波の速さですが、VL=√ghより、VL=√10×4000=200m/秒! これを時速に換算すると
3600秒×200m/秒=7.2×105m/時=720km/時
津波がチリから日本に届くまでの所要時間は
18000km÷720km/時=25時間
画像をクリックすると拡大します
-
岩手県宮古市役所付近
2011.3.11.岩手県宮古を襲った津波
-
同じく宮古市田老地区
この惨状を見て「津波」を歌のタイトルにする・・・。(おことわり。画像は「広報みやこ 平成23年12月1日号No.151」から借用しました。 )

潮汐とは、1日に、2回(1回の時もある)朝に夕に潮が満ちたり、引いたりする現象。
満潮(干潮)1回というのは、次のような事情によります。
満潮(干潮)から次の満潮(干潮)までおよそ12時間25分なので、半日分+25分が次第に加算され1日24時間の中に2回の満潮(干潮)が収まらなくなり、次の日に持ち越されることからおこります。
例えばある港で9月1日11時34分満潮になったとします。12時間25分後に再び満潮になるので、時刻は23時59分で、9月1日は2回満潮となります。次の満潮は23時59分+12時間25分=9月2日12時24分となります(ここまで3回目)。
ところが4回目は、12時24分+12時間25分=9月3日0時49分となって、9月2日は満潮は1回しか起こらないことが分かります。
潮汐の学習にはシーソーで遊ばなくてはならりません(必修)。そしてシーソーで遊ぶためには、バランスの取り方を知らないと遊べません。バランスを取るためには、
重さ✕腕の長さ=腕の長さ✕重さ でした。
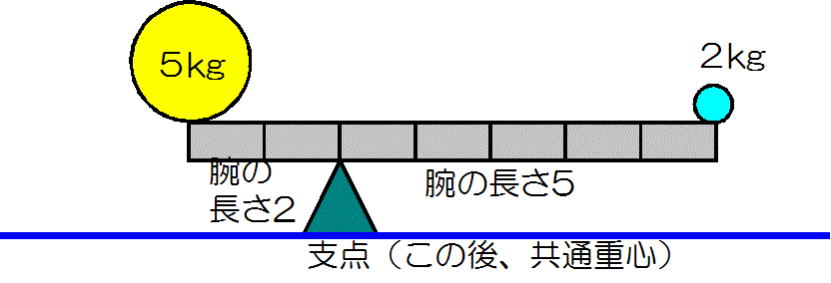
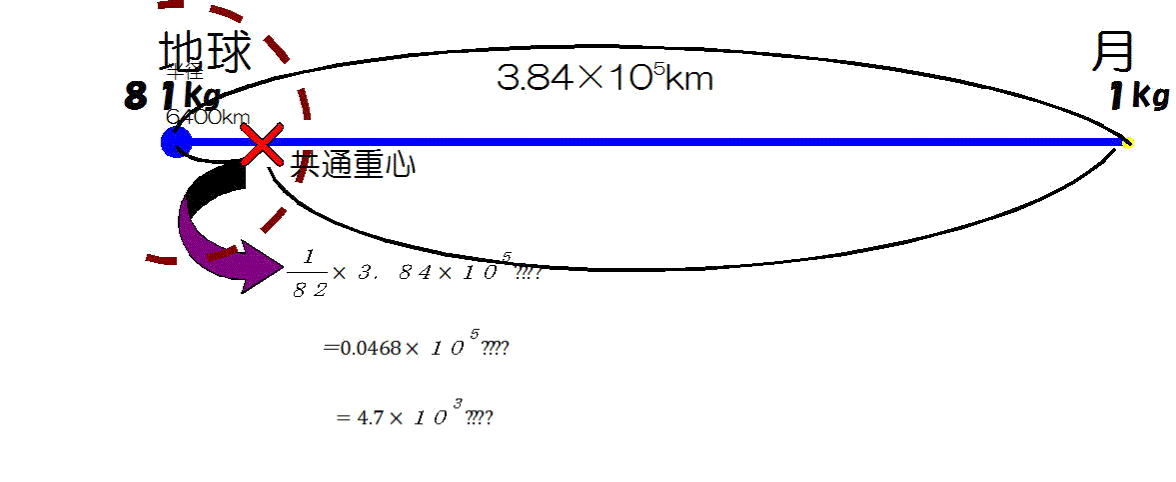
図-1
地球と月がシーソーに乗ってバランスを保つことを考えます。地球の質量は、月の81倍です。図-1で学んだことから、地球はシーソーの支点から1m
の位置に(たとえとして)、月は支点から81mの位置に座ればバランスがとれることになります。
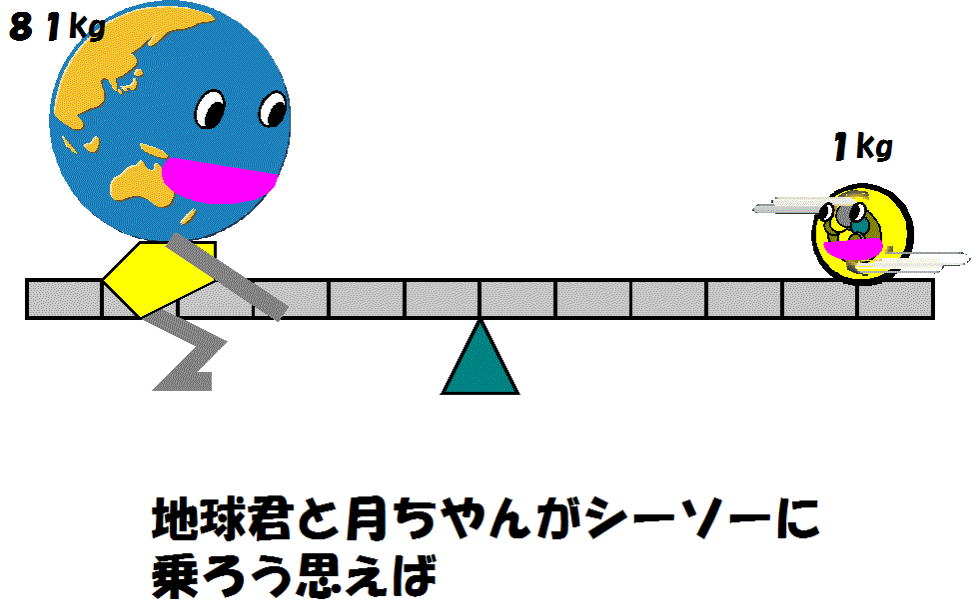
図-2
ところで、実際の地球と月の距離は3.84✕105km、地球の半径は約6400km、月の半径は1700km。
地球の体重(質量)が月のそれの81倍。そのことを考慮し、シーソーの支点(共通重心)がどこになるかというと、図-3のようになります。およそ、地球の中心から3/4地表に向かったところに-地球の内部にシーソーの支点(共通重心)が来てしまいます。
それだけ月が「重い」ことが潮汐に影響していると言えます。
長さ3.84✕105kmのシーソーには地球のサイズが大きくて、乗ることができず、公園で見かけるのどかなシーソーの風景ではなくなるのです。
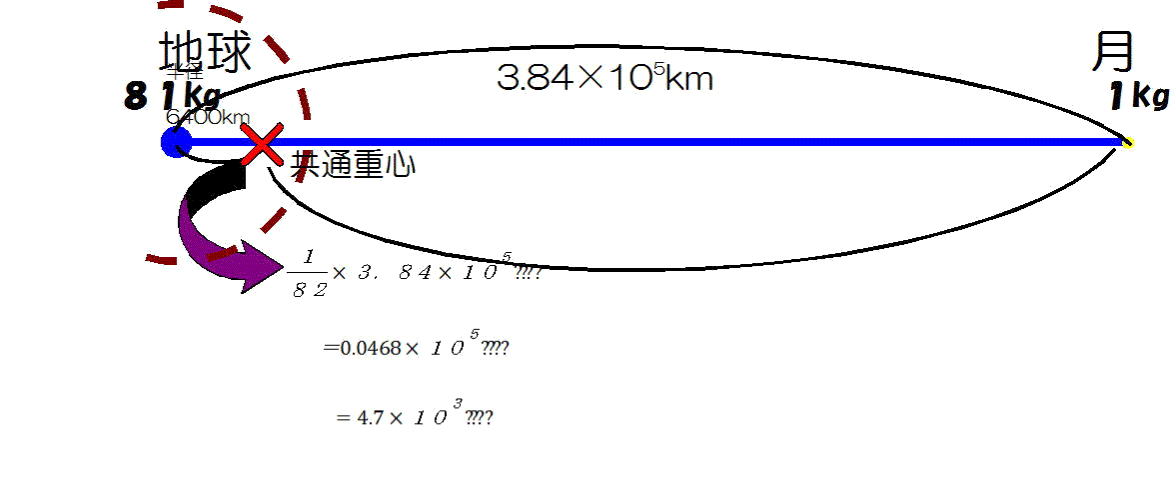
図-3 (図中、「m」が文字バケして「????」となっています。)

図-4
というわけで公園で見られるような、ギッコン・バッタンのシーソーはできそうではありません。

(いちょうの木にリンゴの実はつきません)
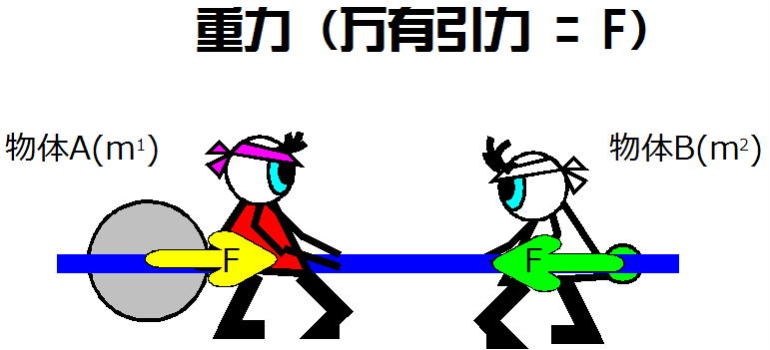
図-5
図-5では断り書きが色々必要で、「赤組ひとみちゃん、白組ひとみちゃん、そして二人が立っている地面(地球も無い)、綱引き(らしき)の綱、以上の質量は『ゼロ』、物体A、物体Bがぽつんとありますよ」ということ-。
物体A(質量m1kg)、物体B(質量m2kg)、2つの物体の中心から距離 r m 離れています。
この時、2つの物体には重力(万有引力=F)が働き、Gを万有引力定数とすると(1式)で表されます。
F=G・m1・m2/r2・(1式)
物体Aは物体Bに対して、自らの方向に近づけようとし、 物体Bは物体Aに対して、自らの方向に近づけようとします。
ところで、物体に力が加えられると物体は変形したり(図-6)、運動状態が変化します(図-7)。

鉄棒に力が加わると

図-6
ゴルフボールに力が加わると


図-7
ゴルフボールはある速度を得ます。
力=加速度✕質量・・・(2式(運動方程式))
の関係から等しい力を加えられたとき、重い(質量大)の物体は(運動)状態の変化が大きくなりません。
一方、軽い(質量小)の物体は(運動)状態の変化が大きくなります。
図-5、(1式)から与えられる万有引力は物体A、物体Bに等しく働きます。すると、力=加速度✕質量・(2式 運動方程式)から質量の小さい(軽い)物体Bが、物体Aより大きな加速度運動を行うことなります。
つまり、地球と月がぽつんと何もない空間にあれば、地球が月に向かって「落下する」のが、月はもっと大きな加速度で地球に向かって「落下する」ことになります。
(同様なことに地球も太陽に向かって「落下」しなければならない。しかし、実際はそうなっていません。)
そこで、地球君と月ちゃんは共通重心周りに公転し、その遠心力と引力と釣り合うことで「近づかず」、「離れもせず」の距離感(間)を保つわけです。
力のつり合う様子は、図-8のようになります。
 |
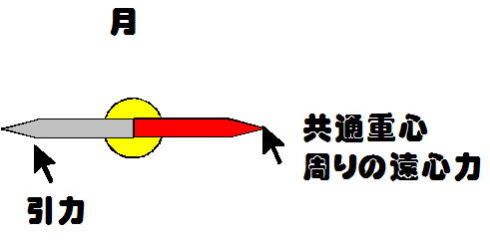 |
図-8
ところで、「地球上のどの地点においても共通重心周りの遠心力の大きさは等しい」
と言われますが、何か分かりにくいことではないでしょうか(図-9)。
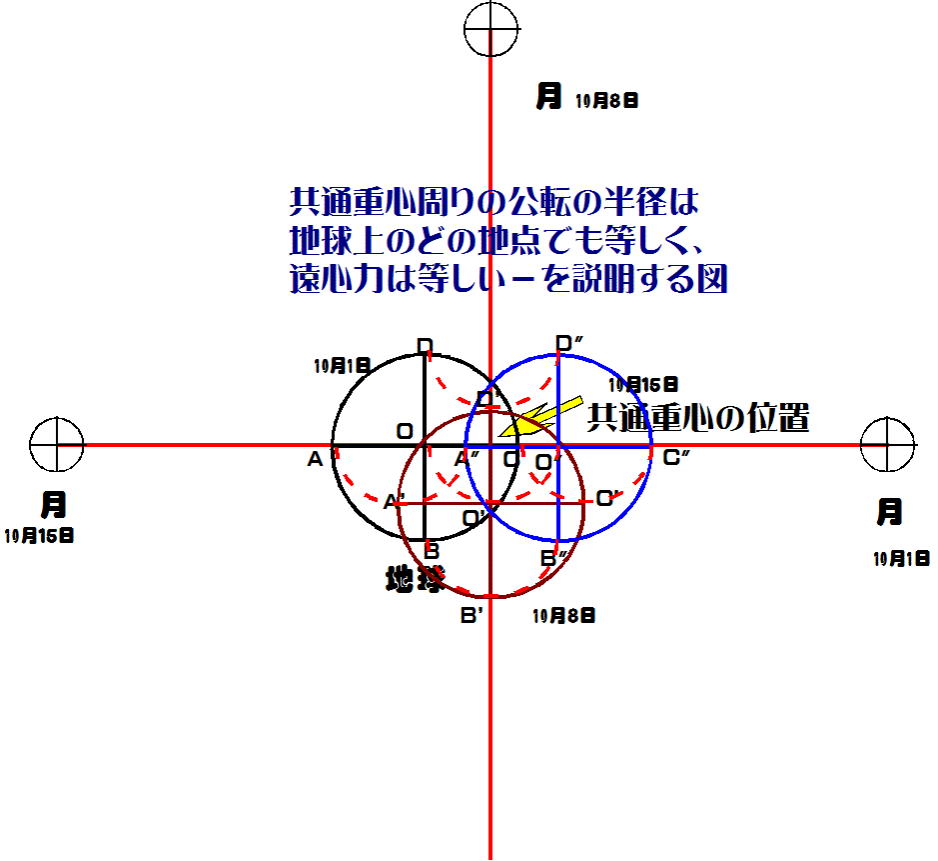
図-9
遠心力
F は F=m r ω2で表されます。
mは回転する物体の質量、 rは円運動するときの半径、 ω(オメガ)は回転の角速度で、1秒間に角度にして何ラジアン(rad)(角度にして何度回転するか-と理解して差し支えありません)回転するかを表します。
いま、地球上の各点で共通重心周りの遠心力の大小比較しようとしています。したがって質量mは一定としなくてはなりません。
また、地球と月の共通重心周りの公転の角速度ωは一定です(27.32日で公転)。となると、円運動の半径 r が一定かどうかをしらべればよいことになります。
図-9の赤の直線の交差点が地球と月の共通重心です。
たとえとして、スタート地点として10月1日の地球(黒色)と月の位置が示されています。約7日後約90度、共通重心周りに公転するので、地球は10月8日頃えんじ色で示された位置に来ます。
ここで注意しなければならないのは、「共通重心を中心に、地球は回転(=自転になってしまう)しない」こと-です。(後述)
したがって、地球上の地点A、B、C、D、Oは、10月8日頃、 それぞれA’、B’、C’、D’、O’の位置に移動することになります。
10月8日頃から更に約7日後の10月15日頃、地球は共通重心周りに公転し、青色で示された位置に来ます。地球上の地点 A’、B’、C’、D’、Oは、それぞれ10月15日頃にはA”、B”、C”、D”、O”に位置します。
以上のように図-9は正確に表せてはいませんが、赤の破線で示した半円AA'A"、半円BB'B"、半円CC'C"、半円DD'D"、半円OO'O"の半径(円運動の半径r)は等しい-と言えます。
つまり、「地球上のどの地点においても共通重心周りの遠心力の大きさは等しい」
ところで、「地球上のどの地点においても共通重心周りの遠心力の大きさは等しい」ことが理解できない場面があるのは、次のような誤解があるためではないかと思われます。
(図-3)
図-3のように教科書には、「地球と月の共通重心が地球の中心からおよそ3/4地表に向かった所にある」と説明されます。
誤解の1つが「×で示されたところに共通重心が固定されている」と思い込んでしまうこと-にあります。
考えて見れば、「引力VS遠心力」の釣り合うところ=×で示される共通重心の位置は、月が移動すればその場所は一か所に固定されるない-ことは理解できます。
地球の中心から地球半径の3/4地表に向かった地点は、沢山あります。つまり、地球の中心から地球半径の3/4で描いた円上(地球・月の中心が含まれる平面=白道面)の一点は、すべて地球と月の共通重心になり得る-からです。
次に「共通重心周りの公転」の「公転」と「自転」がよく理解できていないこと。教科書でも定義を明確に示していない場合が多いです。
フィギャースケートで言えば、「公転」は氷上を体(の軸を中心に)を回転させず(=「自転しない」ということ)回る動き、「自転」は体の軸を中心に回転するような動き-と言えば良いでしょうか。

図-10
図-10は「自転」を示しているひとみちゃん。自転は、「物体」(ひとみちゃんには申し訳ないですが)をとおる軸を中心に回転する運動-と言えます。
したがって、図-3の×の所に軸があり、この軸を中心に回転する運動は自転か?公転か?と考えると自ずと、自転であることが諒解されるでしょう。
余計な説明をするとしたなら、図-3の×を中心に回転する運動は、「地球・月の合体天体」自転でしょう?と言えば納得がいくのではないですか?
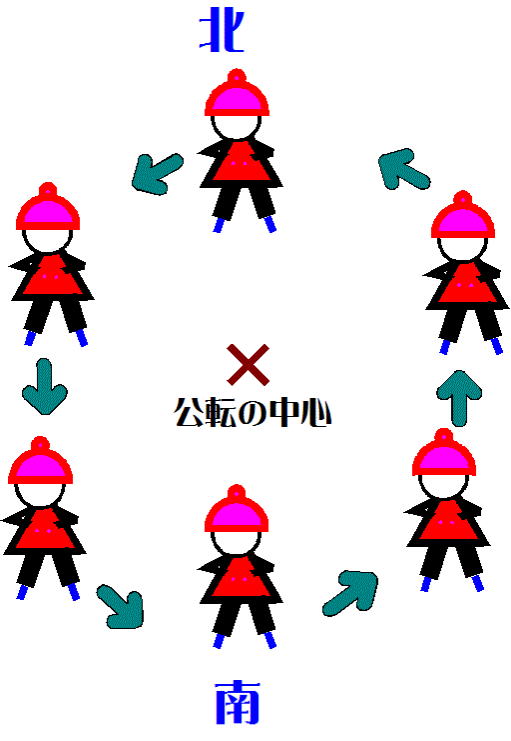
図-11
図-11は「公転」を示しています。公転は、例えば「太陽-惑星系」、「連星系」、「地球-月系」の共通重心を中心(=公転の中心)として、各天体が円ないしは楕円運動を行うこと-と言えます。
図-11では、ひとみちゃん(天体)はスケートをはき、北を向いたまま体を回転させず反時計回りに楕円運動をしています。つまり、ひとみちゃん(天体)は公転している-。
天体(ひとみちゃんの身体)をとおる軸を中心に回転するような「自転」は行っていません-ね。
図-11と図-9を合わせて見て、理解を深めてください。
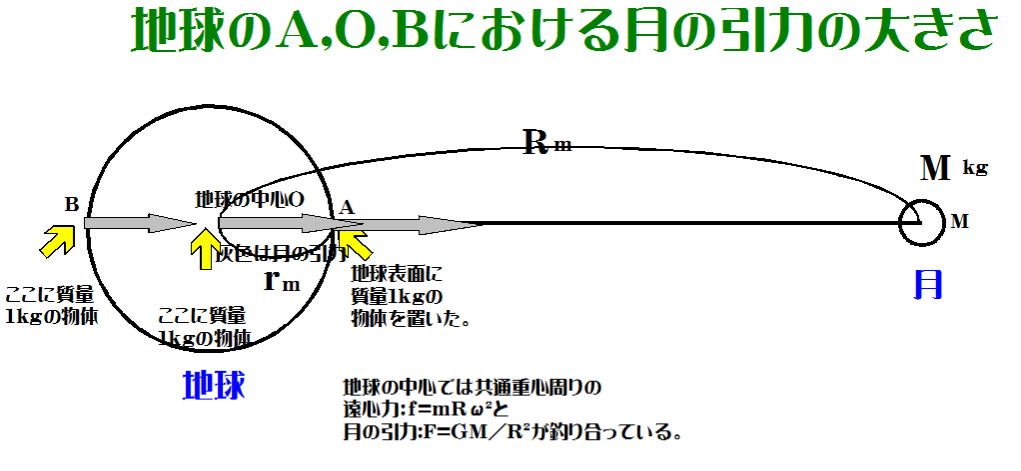
図-12
今ここでは、地球のA,O,B点に質量1kgの物体を置いたとして、それに働く月の引力を求めようとしています。
はじめにO点における月の引力を求めることにします。
(1式)
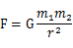
より、 O点における月の引力をFO とすると
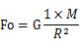
次にA点における月の引力をFAとすると、 A点における質量1kgの物体に及ぶ引力FAは
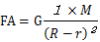
同様に、B点における月の引力をFBとすると、
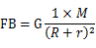
この結果から言えることは、月の引力の大小関係は、
FA>FO>FB となります。
(引力Fは距離の2乗に反比例するから当たり前-と言えばそのとおりになるのですが・・)
潮汐力
潮汐力=地球上、各点に働く月の引力−共通重心周りの遠心力 です。
(図-9)より、遠心力の公式はF遠=m r ω2 。質量1kgの物体に及ぶ遠心力は、m=1kg、F遠=1 r ω2 。
ところが、これに釣り合う力は(図-8)より、月の引力でその大きさは
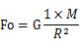
に等しいはずです。(ただし、力の向きは逆向き 図-8)
A点における潮汐力をTAとすると
TA=FA-F遠、TA
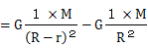
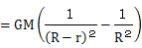
これを -①式、
この式において1/(R-r)2=(R-r)-2、ここで(R-r)=R(1-r/R)なので、1/(R-r)2=(R(1-r/R))-2=R-2(1-r/R)-2
ところで、r=地球の半径、R=地球~月までの距離で、r << R で r/Rは充分小さい値となります。
(1+x)nの式において、xが充分小さいときは(1+x)n≑(1+nx)としてよいことになっています。
したがって、1/(R-r)2=1-(-2)r/R=1+2r/R
∴R-2(1-r/R)-2=R-2(1+2×r/R)=R-2(1+2rR-1)=R-2+2rR-3・・②式
②式は、①式の1/(R-r)2に等しいから、
A点における潮汐力、TAは
TA=GM(1/(R-r)2-1/R2)=GM(1/R2-1/R2+2r/R3)=2GMr/R3-③式
③式はA点における潮汐力、力の向きは月へ向かう
つぎにB点における潮汐力をTBとすると、 TB=F遠-FB、
TB
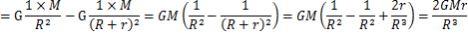
すなわち、A点、B点における潮汐力はその大きさが等しく、働く向きが反対ということになります。
それでは、図-12にC、Dの地点を加えたとして、その地点での潮汐力はどうなるでしょうか?図-13を参照して考えてください。

それでは、図-12にC、Dの地点を加えたとして、その地点での潮汐力はどうなるでしょうか?図-13を参照して考えてください。
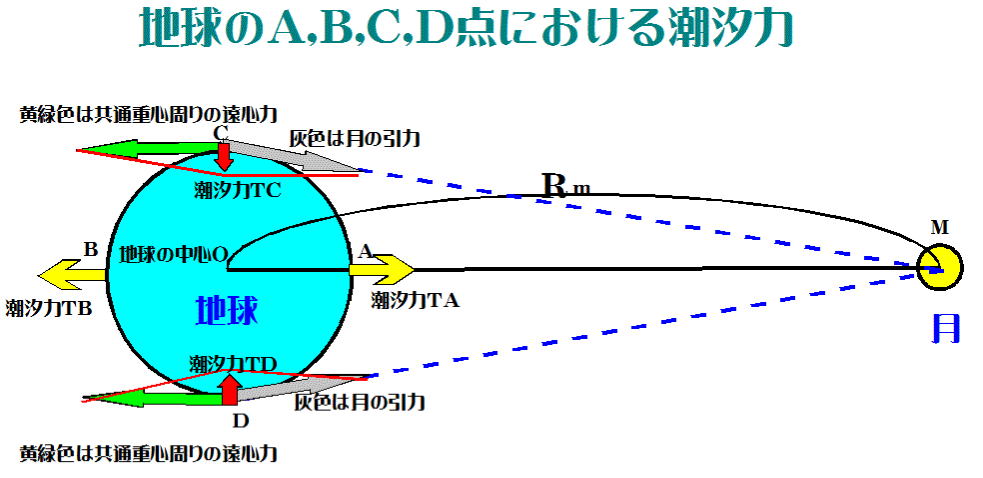
図-13
第一に、地球上の各点での遠心力の大きさはどこでも等しい(かった=既習事項)。(図-9)
第二に、距離MO=距離MC=距離MDとしてよい。地球の中心Oでの月の引力は
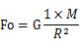
でした。これと共通重心周りの遠心力が釣り合う(合っている)。
地球上のC点、D点では黄緑色の共通重心周りの遠心力と、灰色の月の引力の二つの等しい力の力の平行四辺形が形成されていて、赤で示される矢印がC点、D点での潮汐力になります。
その結果海水は図-14に示されるような挙動を示すことになります。

図-14
このようなことから、月に面した地点でもまた、そこから180度反対の地点でも海水面が上昇し、満潮となります。
一方、およそ90度離れた地点では干潮となります。

「月の起潮力は、太陽のおよそ2倍である」
「月の起潮力は、太暘のおよそ2倍である」ことは、また面倒な話になるのではないかと!そう身構えても仕方がありません
でしょう。まず、確かめてみましょう。
起潮力を求める公式
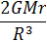
-③式
G=万有引力定数、
M=月、太陽などの質量、
r=地球の半径、
R=地球~月または地球~太陽までの距離。2、G、rは定数としてよいですね。
よって月、太陽の

を比較すればよいですから。
M月=0.012✕地球の質量
R月=3.84✕105km
M太=3.3✕105✕地球の質量、
R太=1.49✕108kmより

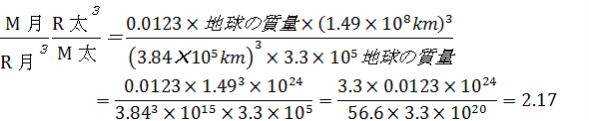
逆に言えば、下の計算のとおりになり、太陽の起潮力は月の約半分ほどで
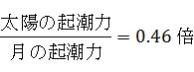
「太陽は潮汐に大きな影響を及ぼす」
地球、月、太陽の位置関係(図-15)で干潮、満潮の差に影響が出て来ます。
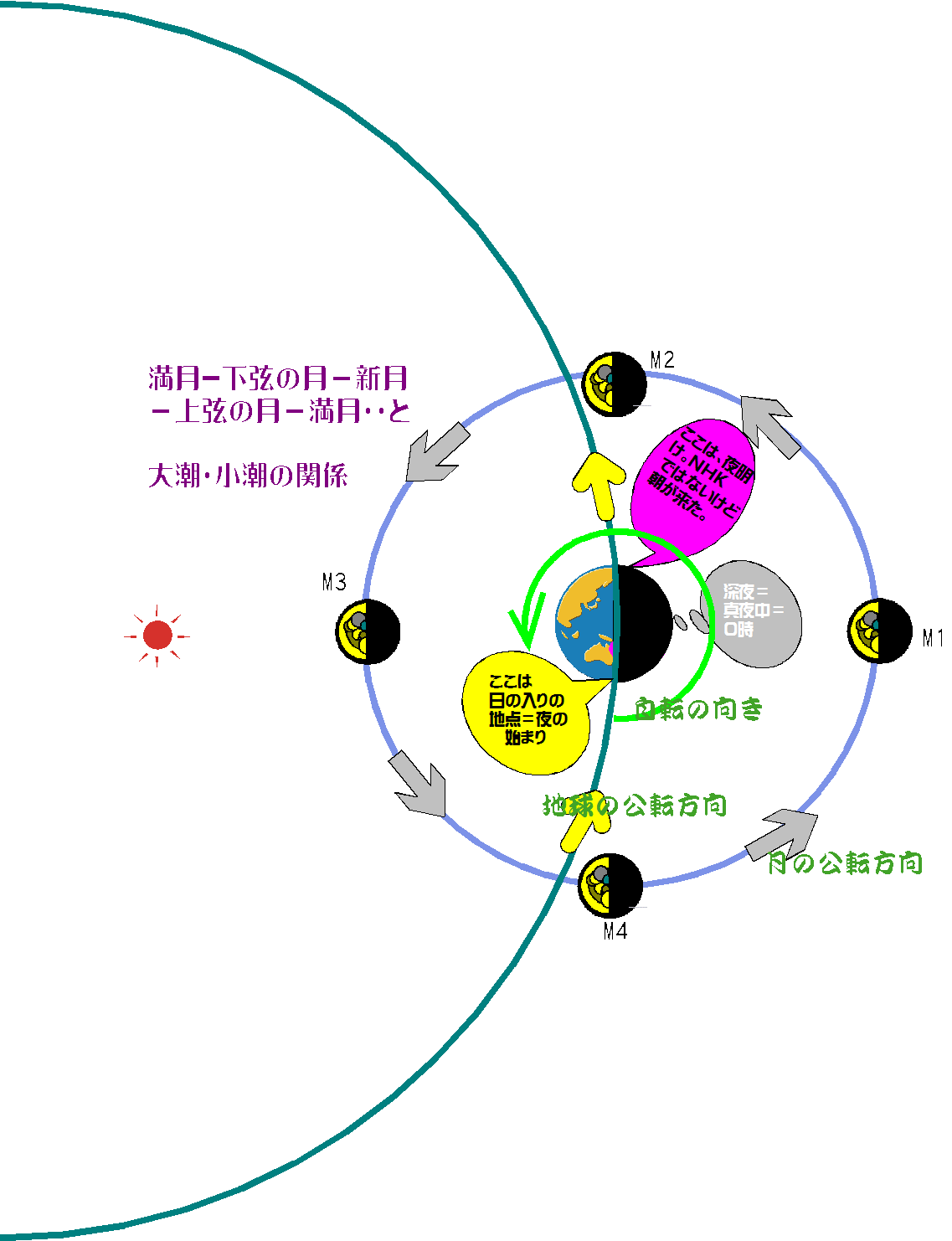
図-15
M1 満月
地球も月も半分は太陽に照らされています。M1のように、太陽-地球-月の順に並んだときは、地球からは丸い月を見ることが出来ることになります。
満月は夕方、東の地平線に上がり、真夜中に南中、明け方西の地平線に沈みます。月は太陽と180度離れているので、互いに反対の方向に位置します。
M2 下弦(の月)
太陽は90度離れており、時間にして6時間(360度自転÷24時間=15度/時間)進んでいます。下弦の月は真夜中に東の地平線に登り、明け方に南中、正午西の地平線に沈みます。
図-15の地球の図は不正確で、ほぼ北極の真上から見た図で、月に向かって右手が西、左手が東となり次のように見えます。

M3 新月
月は太陽と同じ方向にあるために、見ることは出来なく、また太陽と同じ動きを行います。
明け方東の地平線に登り、正午に南中し、夕方西の地平線に沈みます。
M4 上弦(の月)
上弦の月は太陽より90度、6時間進んでいます。正午東の地平線に上がり、夕方南中、真夜中西の地平線に沈みます。上弦の月の見え方は下の図のようになります。

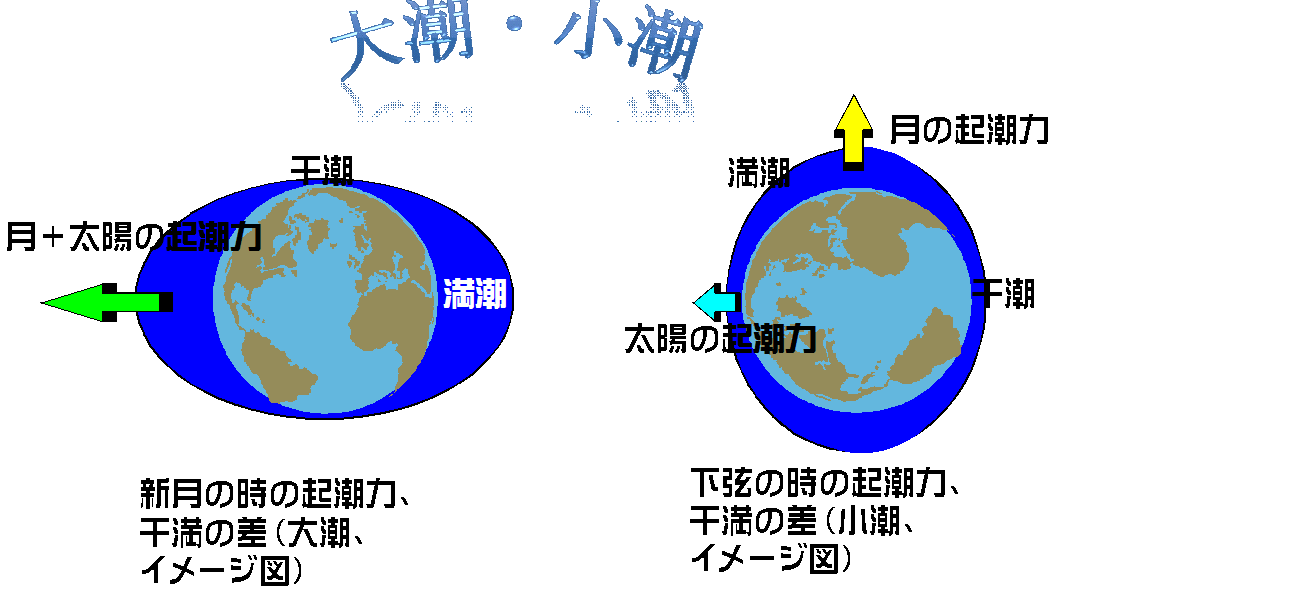
図-16 図-17
大潮(図-16)地球の図には海が描かれていますが、それは置いておき・・。
新月なので月と太陽の起潮力太陽の起潮力が強めあいます。その結果、干潮、満潮の差が大きい大潮となります。
小潮(図-17)一方、図-17は下弦を示していて、月、太陽の起潮力の方向は90度方向にずれています。
この結果、海水は分散され潮差は小さくなります。小潮

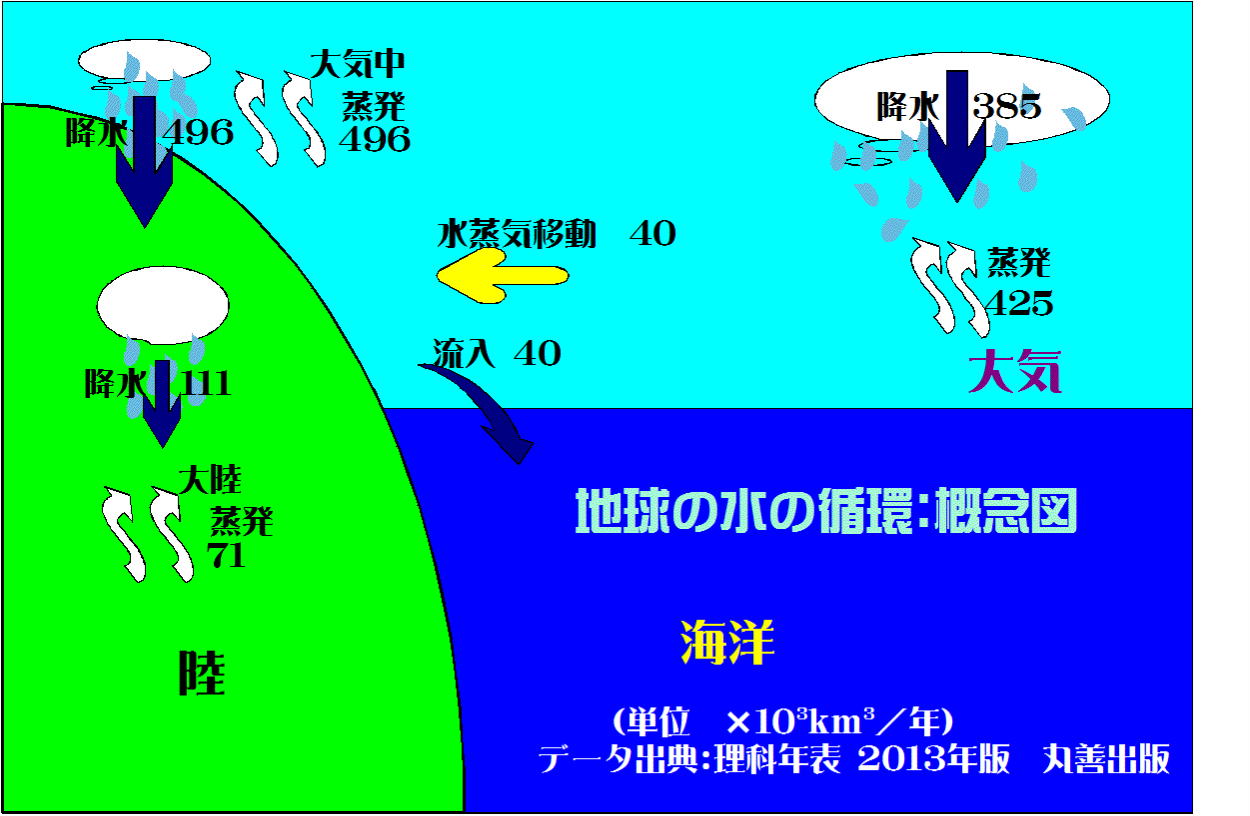
地球表面の30%は陸、70%は海洋でしたね。そして、地球は、水の惑星で水のほとんどは(98%近く)、海水です。
海洋または陸上の液体の水は蒸発し気体(水蒸気)となり、雲(液体・固体)が形成され、雲から雨滴、雪片・氷片が生み出され地表に落下してきます。
それらはそのまま、あるいは融解して流下し再び海洋に循環します。
上は2013年丸善出版理科年表による「地球の水の循環」(表に示されたデータ)を図に表したものです。
地球の水の循環について説明ですが、図左上での「大気中での 蒸発 496(✕103km3/年、以下略) 降水 496」で「? 行き詰まってしまう。」
「大気中で496蒸発して、496降水?。雨滴は地表まで一滴も届かないの?」、「大気中で496蒸発して、496『凝結』」ならば雲が形成されるのだから、まだ理解できるのだが-と考えたり。しかし、データを見るとしっかり「大気中での 蒸発 496 降水 496」とあります。
まず、蒸発、降水の収支は一致しているのでこれ以上騒がないことに・・・。
次に大陸での蒸発、降水の収支について。大陸では「蒸発 71 降水 111」で40「雨が降りすぎている」。このままでは陸は水浸しになってしまいます。111-71=40の雨水は海に流れます。71しか蒸発しないのに111降水があるのは、海洋から40の水蒸気が大陸に移動してくるためです。
海洋では「蒸発 425 降水 385」でこのままでは海が干上がってしまいます。不足の40は大陸からもたらされるから-ぴったりです。
以上のように水蒸気の移動、河川水の流入によって大陸が水浸しにならず、また海面の高さに変動が起こることが無く一定に保たれていることになります。
地球の水の98%は海水と前にお話をしました。では、淡水の割合はどのようになっているのでしょうか?下の資料は国土交通省のHP水資源から借用しました。
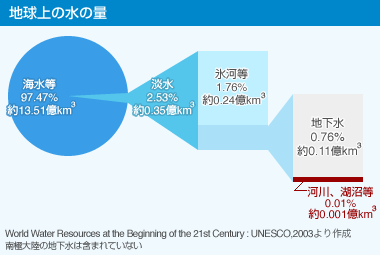
淡水の大部分は氷雪になります。考えればグリーンランドや広大な南極大陸、アルプス・ヒマラヤなど高山の氷河を考えれば氷雪が最も多いと考えられます。
2番目が地下水で、目に触れないことだけあって意外な感じがあります。
国土交通省のHPによれば人類が利用しやすい水は淡水のわずかに0.001%とのことで、これを「宇宙線地球号」という閉じた空間で使っているわけですから、汚染させないようにしなければなりません。
南極大陸・昭和基地付近の氷
南極では雪が降り積み、次第に下の方から自重で氷になっていきます。氷になって海氷になるまで2~4万年かかると言われています。(砕氷艦しらせ・南極大陸・昭和基地付近の氷 展示パンフレット説明文による)雪と雪の間に含まれた堆積した当時の空気も氷の中に閉じ込められるため、氷の中には小さい泡が含まれます。南極の氷がとけるとその泡がはじけて「パチパチ」と音をたてます。2~4万年前というと更新世の終わり頃、クロマニョン人が出現するあたりから縄文時代が始まるころ、それとおなじ空気をすこしながら吸ったことになります。
(岩手・盛岡 子ども科学館のイベント 「南極の氷がやってくる!~海上自衛隊観測船『しらせ』からの贈り物~)
national park、designate 、specify、transparent、clear、cape、famous、well-known、quasi national park、farm produce、agricultural products、important、different、(n:difference)、organic compound、organic material、emphasize、(n:emphasis)、enough、refract、(n:refraction)、perceive、ultraviolet rays、visible ray、ultrared rays、electric wave、radiate、molecule、collide with~、scattered about ~、synthetic、synthesized、density、concentration、evaporation、conductivity、regulation、(v:regulate)、adjustment、(v:adjust)、photo synthesis、absorption、(v:absorb)、curved line、for example、stir、trade wind、cause、effect 、tide、natural phenomenon、high tide、(full tide)、ebb tide、(low tide )、transformation、(modification)、state、(situation)、motion、centrifucal force、attraction、gravitation、acceleration、revolution、spin、(rotation)、definition、(v: define)、new moon、full moon、sunrise、sunset、spring tide、neap tide、circulation、notion、(general idea)





