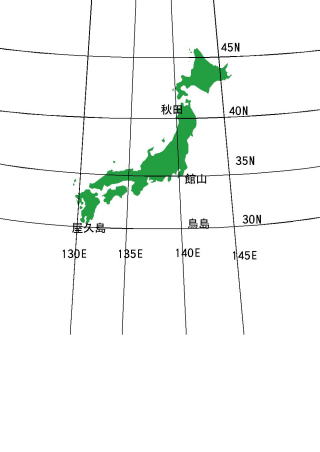
秋田・館山は東経140度の経線上に位置し543kmの距離、鳥島と屋久島は北緯30度の緯線上に位置し944kmの距離にあるものとして計算しなさい。

　Q1 エラトステネスの方法に従って、北極－南極を巡る地球全周の長さ、極半径(b)を求めよ。
　

　Q2　鳥島、屋久島のデータを活用し、赤道半径(a)を求めよ。


　Q3　地球の扁平率（＝(a-b)/a）を分数の形（1/○○○）で示せ。


【解説・解答】

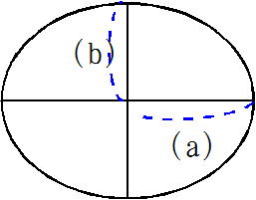
　地球は自転しているため、遠心力が働きその結果「球」ではなく南北両極方向に短く、

赤道方向に伸びた「回転楕円体」となっている。

　地球中心から赤道までを赤道半径（(a)）、地球中心から極までを極半径（(b)）とし、

扁平率（つぶれの度合い f ）を f＝(a-b)/a、普通 f＝1/○○○として表す。

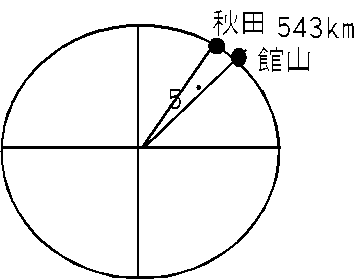
A1　扇形の中心角が5°、弧の長さが543km。極半径を(b)とすると、地球全周の長さは

2π(b)。扇形の中心角と弧の長さは比例するので、

2π(b)：360°＝543km：5°

2π(b)＝360°/5°✕543km

＝72✕543km

＝39096km、「有効数字３桁」で表すと、「４桁目」を四捨五入するので、

答え　地球全周の長さ　39100km
　　　　　　　　　　　　
または　　 3.91✕10４km

極半径(b)は、

2π(b)＝39096km

(b)＝39096km/2π

＝39096/6.28km

＝6225.4km

答え 極半径(b) 6.23✕10３km


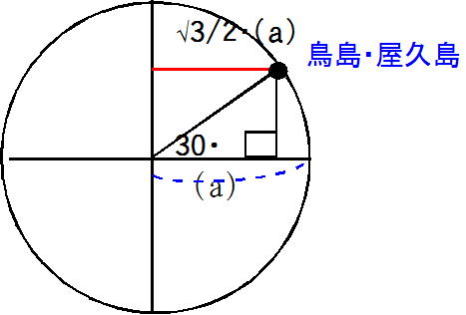
A2　鳥島・屋久島を通る緯線は赤道より短い。赤道半径を(a)とすると、鳥島・屋久島

を通る緯線＝2✕π✕√3/2✕(a) 　（2πｒの公式）再び

2✕π✕√3/2✕(a)：360°＝944km：10°

(a)について解いて、

答え　赤道半径(a)6.25✕10３km

A3

f＝(a-b)/a　より

＝（6.25✕10３km － 6.23✕10３km）/ 6.25✕10３km

＝0.02/ 6.25
分子、分母を0.02で割って

＝1/312.5

答え 1/313